Построение геометрии любой детали в SolveSpace начинается с проектирования эскиза (sketch). Эскиз представляет собой набор замкнутых контуров (циклов, loop), каждый из которых не должен иметь самопересечений и пересечений с другими контурами. Контуры состоят из примитивов (entity). Примитивы объединяются в контуры с помощью ограничения "точка-к-точке" (points coincident).
Часть 1
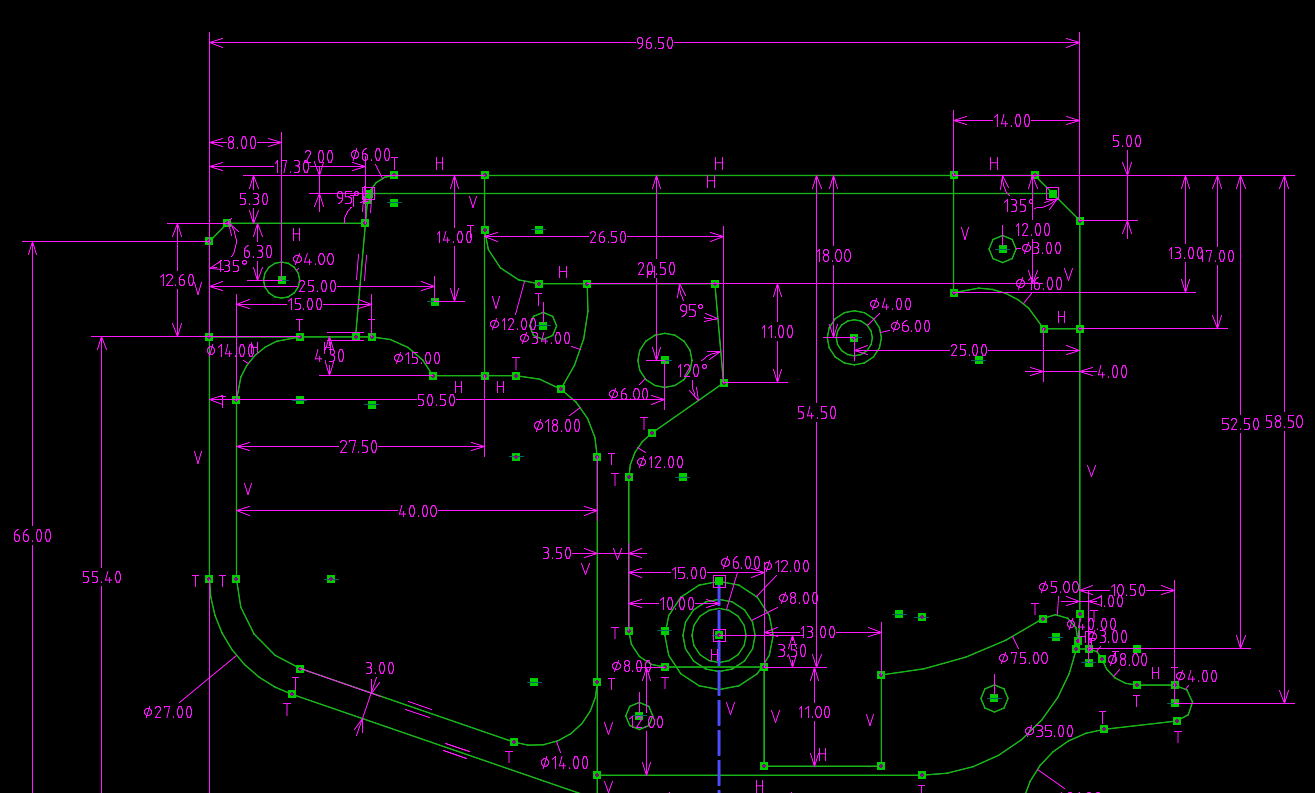
Запрос (request)
Создание примитивов в SolveSpace имеет одну особенность: пользователь создает их наборами (запросы, requests). Например, при запросе на создание отрезка создаются три сущности для его представления: две точки и линия, соединяющая их. Для пользователя не существует разделения запроса на отдельные сущности: если пользователь удаляет одну из сущностей запроса, удаляется и весь запрос. Сущности можно разделить на два класса: те, которые не имеют параметров (parameters) и сущности, имеющие параметры: точки, нормали и расстояния.
Точки
Точки в SolveSpace являются основой параметризации и имеют параметры, соответствующие координатам в Декартовой системе. Точки бывают двумерные и трехмерные и содержат два или три параметра соответственно. Для простоты, будем рассматривать такие характеристики, как число параметров, степеней свободы (degrees of freedom, DOF) и уравнений только для двумерного случая.
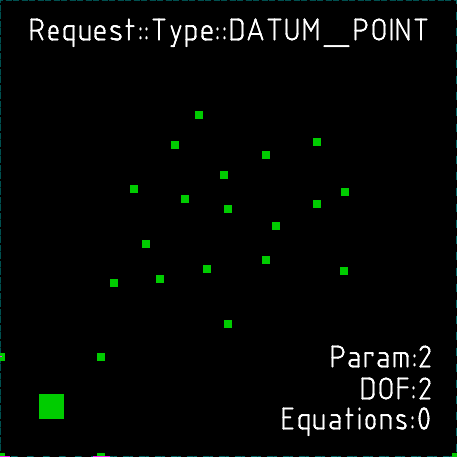
Нормали
Нормаль имеет ссылку на точку, определяющую начало системы координат (origin). Нормали используются для задания системы координат в сборках деталей (assembly) и для некоторых примитивов. Пользователь не может создавать нормали. Нормаль вводит 4 параметра и одно уравнение (equation), что соответствует 3 вращательным степеням свободы. Этот поворот выражается кватернионом, а уравнение служит для приведения его к единичной длине.
Расстояния
Расстояния служат для задания радиусов окружностей. Эта сущность не имеет визуализации, и ее невозможно создать отдельно, поэтому ее можно рассматривать как часть окружности. Сущность расстояния определяет единственный параметр — радиус окружности.
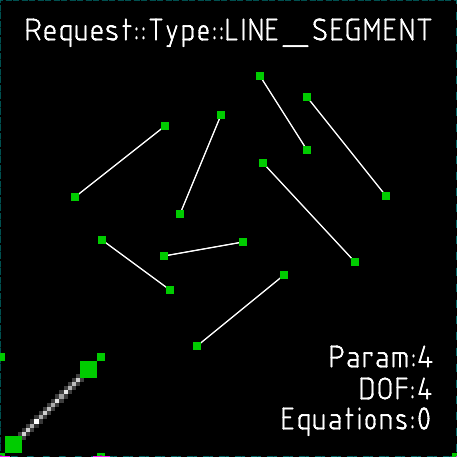
Отрезки
Отрезок состоит из двух точек и линии, которая их соединяет. Отрезок вводит 4 степени свободы и 4 параметра.
Окружности
Запрос на создание окружности создает точку, нормаль, расстояние и линию окружности. Нормаль нужна для ориентации окружности в трехмерном пространстве.

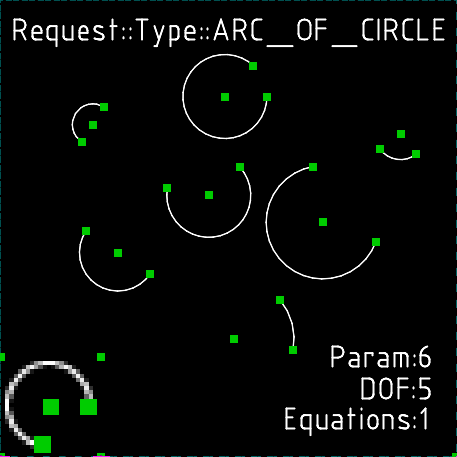
Дуги окружностей
Запрос на создание дуги окружности состоит из трех точек, нормали и отрезка окружности. Дуга добавляет шесть параметров и одно уравнение. Результирующее число степеней свободы — пять. Их можно представить как координаты центра, радиус, одномерные координаты (углы) начала и конца дуги.
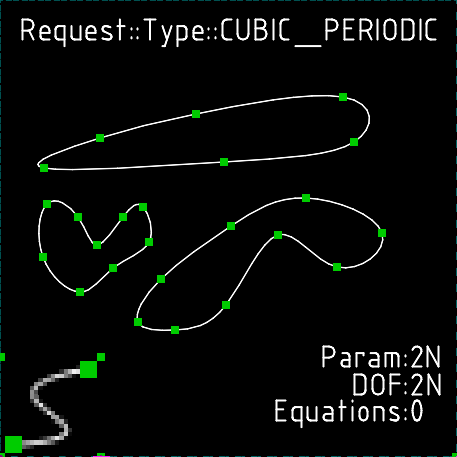
Кубические сплайны Безье
В SolveSpace существует возможность создания кубических сплайнов Безье. Сплайны могут быть замкнутые и незамкнутые. Если сплайн содержит более, чем 4 точки, создается несколько отрезков кубических сплайнов, с гладкой стыковкой первых и вторых производных. Например, такие сплайны идеально подходят для проектирования аэродинамического профиля крыла самолета и других обтекаемых форм. Для незамкнутого сплайна имеется возможность изменять производные в начале и конце сплайна с помощью изменения координат соответствующих точек.

Текст
SolveSpace поддерживает создание контуров на основе текста с использованием шрифтов формата TrueType, которые тоже основаны на кубических сплайнах. Это позволяет создавать надписи на объемных моделях деталей.

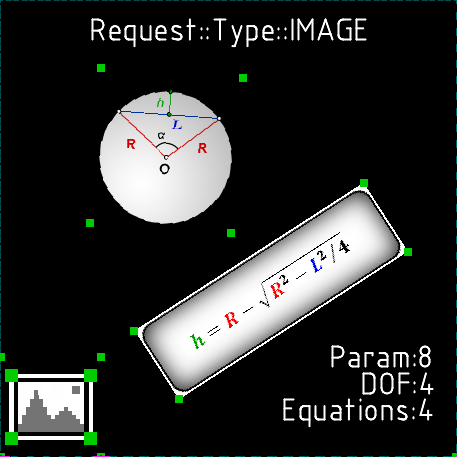
Изображения
Существует возможность вставки произвольного изображения из файла формата png. Это изображение можно свободно вращать, изменять его размеры, благодаря чему оно может служить основой для ручного конвертирования отсканированных чертежей в формат SolveSpace. Угловые точки изображений могут быть задействованы в ограничениях, что позволяет выравнивать изображение и настраивать его масштаб.
Заключение
Здесь я кратко познакомил вас с основными типами сущностей двумерного эскиза SolveSpace. Эти знания будут активно использоваться в следующей статье, где будут рассмотрены уравнения ограничений.
Автор: FadeToBlack

