Всем привет. В этой статье я расскажу вам о нейронных сетях в кратком виде. Мы рассмотрим строение искусственных нейронов, многослойные сети, метод обратного распространения ошибки.

Нейронные сети решают огромное количество задач. Самые основные — классификация и прогнозирование.
Например, мы хотим узнать количество баллов за тест, основываясь на том, сколько часов мы учились и спали. Такая задача будет относится к прогнозированию, так как мы предсказываем нашу оценку. А ещё — это будет называться контролируемой регрессией.
Если бы мы хотели узнать «буквенную оценку» за тест — это бы называлось классификацией.
Строение нейронных сетей
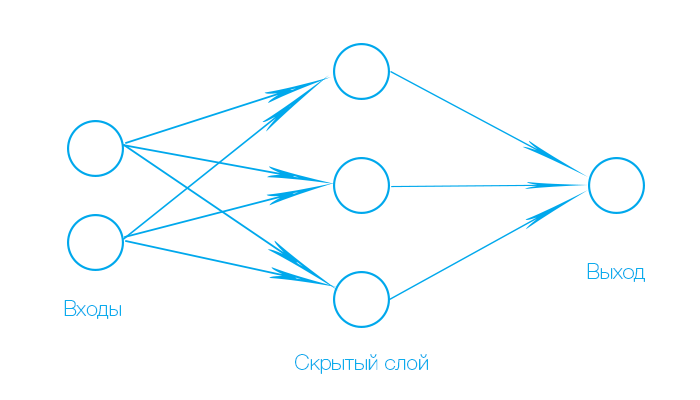
Любая искусственная нейронная сеть состоит из слоёв. Первый слой — входной, последний — выходной.
Во входном слое расположены 'нейроны', которые принимают сигнал, но не обрабатывают его. Количество 'нейронов' в этом слое зависит от количества данных. Например, мы подаём на нашу сеть запах цветка и яркость его цвета. В таком случае будет два входных нейрона.

В выходном слое располагаются нейроны, которые обрабатывают сигнал и выдают во внешнюю среду. Количество нейронов в нём может быть разное. В случае с цветком — один выходной нейрон, потому что мы хотим узнать, хороший он или нет.
Любой слой, расположенный между входным и выходным — скрытый. В нём находятся нейроны, которые обрабатывают информацию полученную с предыдущих слоёв или входного, и передают на следующий или выходной. Их количество может быть разное.
В задаче, где мы хотели получить количество баллов за тест — два входных 'нейрона', три скрытых и один выходной.
Стрелочки передающие сигналы — синапсы. Они выполняют простую функцию — умножают входной сигнал на синаптический вес. Нейроны выполняют более сложную функцию — складывают результаты синапсов и выводят через функцию активации. Мы будем использовать самую основную — сигмоиду. Она преобразует суммарный результат нейрона в вид от 0 до 1.
Выглядит она так: 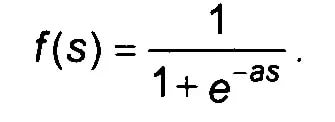
e — это экспонента(показательная функция, по-другому «exp»), -as — суммарный результат нейрона.
Таким образом мы получаем такую модель нейрона:
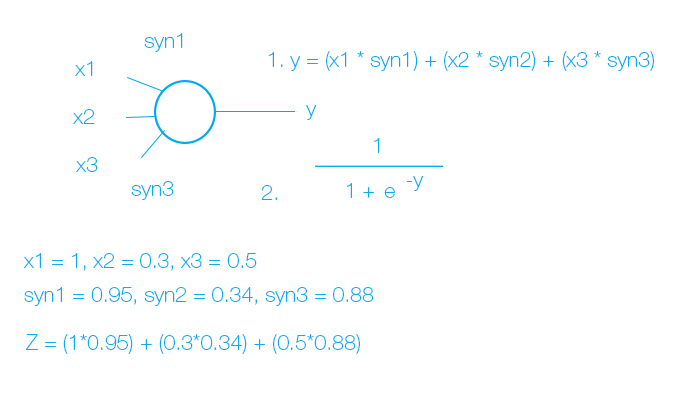
Прежде чем подать данные на нейронную сеть — нужно их нормализовать. Это делается из-за того, что нейронная сеть не способна различать единицы измерения.
Данные приводятся к виду от 0 до 1. Это делается простым способом. Мы берём каждое входное число, которое мы подадим на сеть, и делим его на максимальное число из входных данных.
Чтобы нормализовать выходные данные — мы делим каждое выходное значение на максимальное в его единицах измерения. Допустим, данные идут от 0 до 100, в таком случае мы делим наше выходное значение на 100. Нормализация выходных данных проводится при обучении.
Чтобы перевести выходное число обратно в наши единицы измерения, нужно умножить выходное число на то число, на которое мы делили. В нашем случае на 100.
Обучение нейронных сетей — достаточно сложная часть. Рассмотрим на задаче «Оценка за тест».
Чтобы обучить нейронную сеть, мы должны иметь уже готовую таблицу входных и выходных данных. Такая таблица называется обучающей выборкой.
Обучение — процесс, при котором изменяются синаптические веса, чтобы нейронная сеть выдавала более правильное значение.
Обратное распространение ошибки — самый лучший метод. Сначала мы вычисляем ошибку, затем распространяем её от выхода по синапсам к скрытым слоям. То есть ошибка умножается на синаптические веса. Модифицированные ошибки хранятся в каких-либо переменных или массивах. Чтобы начать менять веса благодаря этим ошибкам, применяют формулу дельта-правила.
Где n — скорость обучения(часто не используют), error — ошибка, input — входное значение.
Например, у выходного нейрона входными значениями будут являться значения, которые пришли со скрытых нейронов. Для скрытых нейронов входные значение — значения пришедшие с входного слоя(в нашем случае)
Практика
Напишем нашу первую задачу с оценкой. Будем программировать на языке Python, используя библиотеку numpy.
Составим обучающую выборку входных данных и выходных данных для того, чтобы обучить нейронную сеть.
import numpy as np
X = np.array([[3,5],[5,1],[10,2]])
# обучающая выборка входных и выходных данных
y = np.array([[75, 82, 93]]).T
Проводим нормализацию данных. Входные данные измеряются в часах, а выходные от 0 до 100. Как я говорил, нейронная сеть не способна понять такой разницы. Входные данные делим на максимальное из них число, а выходные делим на 100, так как они измеряются в пределах до 100.
X = X / np.amax(X, axis = 0)
y = y / 100
Теперь создадим синапсы нашей нейронной сети. Так как у нас три скрытых нейрона и два входа, то у каждого скрытого нейрона будет по 2 синапса, в общем количестве — 6. Для этого составим двумерную матрицу, заполнив её случайными числами от 0 до 1. У выходного нейрона три синапса, так как три скрытых нейрона передают ему сигнал. Тоже создадим матрицу со случайными значениями.
synapses_hidden = 2 * np.random.random((2,3)) - 1
synapses_output = 2 * np.random.random((3,1)) - 1
Начинаем обучать нашу нейронную сеть. Подаём ей данные из обучающей выборки, получаем ответ, вычисляем ошибку, распространяем её и корректируем веса по дельта правилу.
Обучать будем 10000 раз. Думаю этого хватит.
Подаём данные и вычисляем ответ. np.dot перемножает матрицы и затем полученные значения.
np.exp — та самая экспонента для функции активации.
for j in range(10000):
l0 = X
# Входной слой ( 2 входа )
l1 = 1 / (1 + np.exp(-(l0.dot(synapses_hidden))))
# Скрытый слой ( 3 скрытых нейрона )
l2 = 1 / (1 + np.exp(-(l1.dot(synapses_output))))
# Выходной слой ( 1 выходной нейрон )
Продолжаем выполнять в том же цикле. Тут delta правило немного выглядит по-другому. Но принцип остаётся тем же.
l2_delta = (y - l2) * (l2 * (1 - l2))
# вычисляем ошибку и используем дельта-правило
l1_delta = l2_delta.dot(synapses_output.T) * (l1 * (1 - l1))
# получаем ошибку на скрытом слое и используем дельта-правило
synapses_output += l1.T.dot(l2_delta)
# корректируем веса
synapses_hidden += l0.T.dot(l1_delta)
# корректируем веса от входов к скрытым нейронам
Теперь нам остаётся вывести ответ. Переводим ответ нейронной сети в наши единицы измерения. Так как мы делили на 100 в обучающей выборке выходных данных, тот тут на 100 мы умножаем. l2 — выходной слой, выводим с него значение.
print(l2 * 100)
В итоге мы получаем такие вот ответы:
[[ 75.00483985]
[ 82.53359502]
[ 92.09079581]]
Как видите, ответы приблизительные. На практике вы можете округлять их. После обучения вы можете подавать свои данные, нейронная сеть будет стараться выдавать правильный ответ.
Спасибо за внимание. Скоро выпущу обещанную статью о рекуррентных нейронных сетях.
В этой статье использовались примеры из видео Neural Networks Demystified, так же был использован пример нейронной сети из статьи «Нейросеть в 11 строчек на Python»
Автор: EmeraldSoft