Главная

Простая программа на Python для гиперболической аппроксимации статистических данных

2017-03-01 в 8:21, admin, рубрики: python, аппроксимация, метод наименьших квадратов

Зачем это нужно

Законы Зипфа оописывают закономерности частотного распределения слов в тексте на любом естественном языке[1]. Эти законы кроме лингвистики применяться также в экономике [2]. Для аппроксимации статистических данных для объектов, которые подчиниться Законам Зипфа используется гиперболическая функция вида:

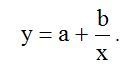Простая программа на Python для гиперболической аппроксимации статистических данных - 1 (1)

где: a.b – постоянные коэффициенты: x – статистические данные аргумента функции (в виде списка): y- приближение значений функции к реальным данным полученным методом наименьших квадратов[3].

Обычно для аппроксимации гиперболической функцией методом логарифмирования её приводят к линейной, а затем определяют коэффициенты a,b и делают обратное преобразование [4]. Прямое и обратное преобразование приводит к дополнительной погрешности аппроксимации. Поэтому привожу простую программу на Python, для классической реализации метода наименьших квадратов.

Алгоритм

Исходные данные задаются двумя списками 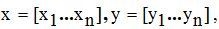Простая программа на Python для гиперболической аппроксимации статистических данных - 2 где n ─ количество данных в списках.

Получим функцию для определения коэффициентов 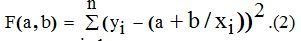Простая программа на Python для гиперболической аппроксимации статистических данных - 3

Коэффициенты a,b найдём из следующей системы уравнений: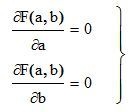 Простая программа на Python для гиперболической аппроксимации статистических данных - 4 (3)

Решение такой системы не представляет особого труда:

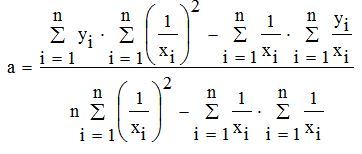Простая программа на Python для гиперболической аппроксимации статистических данных - 5 (4),
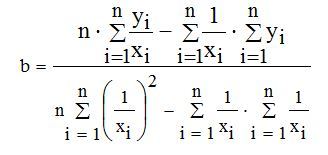(5).

Средняя ошибка аппроксимации 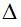Простая программа на Python для гиперболической аппроксимации статистических данных - 7 по формуле: 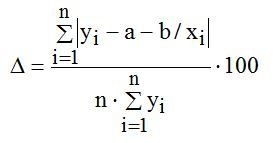(6)

Код Python

#!/usr/bin/python
# -*- coding: utf-8 -*
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
def mnkGP(x,y): # функция которую можно использзовать в програме
              n=len(x) # количество элементов в списках
              s=sum(y) # сумма значений y
              s1=sum([1/x[i] for i in  range(0,n)]) #  сумма 1/x
              s2=sum([(1/x[i])**2 for i in  range(0,n)]) #  сумма (1/x)**2
              s3=sum([y[i]/x[i]  for i in range(0,n)])  # сумма y/x                   
              a= round((s*s2-s1*s3)/(n*s2-s1**2),3) # коэфициент а с тремя дробными цифрами
              b=round((n*s3-s1*s)/(n*s2-s1**2),3)# коэфициент b с тремя дробными цифрами
              s4=[a+b/x[i] for i in range(0,n)] # список значений гиперболической функции              
              so=round(sum([abs(y[i] -s4[i]) for i in range(0,n)])/(n*sum(y))*100,3)   # средняя ошибка аппроксимации
              plt.title('Аппроксимация гиперболой Y='+str(a)+'+'+str(b)+'/xn Средняя ошибка--'+str(so)+'%',size=14)
              plt.xlabel('Координата X', size=14)
              plt.ylabel('Координата Y', size=14)
              plt.plot(x, y, color='r', linestyle=' ', marker='o', label='Data(x,y)')
              plt.plot(x, s4, color='g', linewidth=2, label='Data(x,f(x)=a+b/x')
              plt.legend(loc='best')
              plt.grid(True)
              plt.show()
x=[10, 14, 18, 22, 26, 30, 34, 38, 42, 46, 50, 54, 58, 62, 66, 70, 74, 78, 82, 86] 
y=[0.1, 0.0714, 0.0556, 0.0455, 0.0385, 0.0333, 0.0294, 0.0263, 0.0238, 0.0217,
   0.02, 0.0185, 0.0172, 0.0161, 0.0152, 0.0143, 0.0135, 0.0128, 0.0122, 0.0116] # данные для проверки по функции y=1/x
mnkGP(x,y)

Результат

Простая программа на Python для гиперболической аппроксимации статистических данных - 9

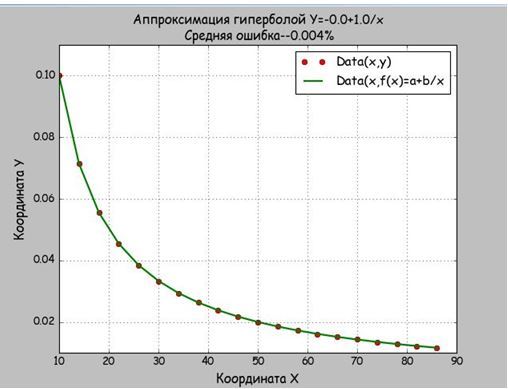
Мы брали данные из функции равносторонней гиперболы, поэтому и получили a=0,b=10 и абсолютную погрешность в 0,004%. Значить функция mnkGP(x,y) работает правильно и её можно вставлять в прикладную программу

Аппроксимация для степенных функций

Для этого в Python есть модуль scipy, но он не поддерживает отрицательную степень d полинома. Рассмотрим код реализации аппроксимации данных полиномом.

#!/usr/bin/python
# coding: utf8
import scipy as sp
import matplotlib.pyplot as plt
def mnkGP(x,y):
              d=2 # степень полинома
              fp, residuals, rank, sv, rcond = sp.polyfit(x, y, d, full=True) # Модель
              f = sp.poly1d(fp) # аппроксимирующая функция
              print('Коэффициент -- a %s  '%round(fp[0],4))
              print('Коэффициент-- b %s  '%round(fp[1],4))
              print('Коэффициент -- c %s  '%round(fp[2],4))
              y1=[fp[0]*x[i]**2+fp[1]*x[i]+fp[2] for i in range(0,len(x))] # значения функции a*x**2+b*x+c
              so=round(sum([abs(y[i]-y1[i]) for i in range(0,len(x))])/(len(x)*sum(y))*100,4) # средняя ошибка
              print('Average quadratic deviation '+str(so)) 
              fx = sp.linspace(x[0], x[-1] + 1, len(x)) # можно установить вместо len(x) большее число для интерполяции
              plt.plot(x, y, 'o', label='Original data', markersize=10)
              plt.plot(fx, f(fx), linewidth=2)
              plt.grid(True)
              plt.show()

x=[10, 14, 18, 22, 26, 30, 34, 38, 42, 46, 50, 54, 58, 62, 66, 70, 74, 78, 82, 86] 
y=[0.1, 0.0714, 0.0556, 0.0455, 0.0385, 0.0333, 0.0294, 0.0263, 0.0238, 0.0217,
   0.02, 0.0185, 0.0172, 0.0161, 0.0152, 0.0143, 0.0135, 0.0128, 0.0122,
   0.0116] # данные для проверки по функции y=1/x
mnkGP(x,y)

Результат

Простая программа на Python для гиперболической аппроксимации статистических данных - 10
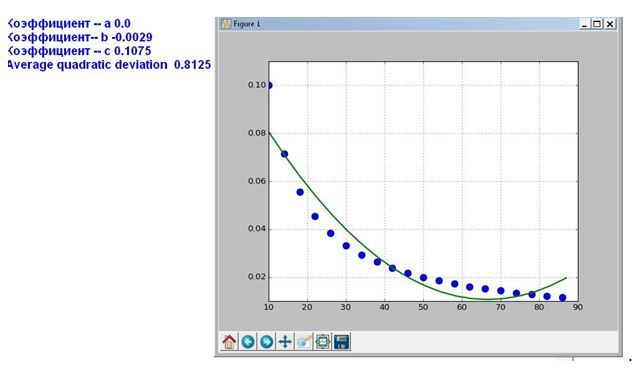
Как следует из графика, при аппроксимации параболой данных изменяющихся по гиперболе средняя ошибка возрастает, а свободный член квадратного уравнения обращается в ноль.