Привет, хабрахабр.
Листая одним декабрьским вечером различные хабы, я заметил, что нигде давненько не бывало статей о реверсинге. А разборов crackme/keygenme – и подавно. И вдруг меня осенило: почему бы не написать свой туториал?
Тех, кого интересует разбор простенького криптографического keygenme и что же в итоге получилось, прошу под кат.
Сегодня мы будем препарировать keygenme под названием «The XOR Algorithm» авторства Ksydfius. Найти данный keygenme вы можете на сайте crackmes.de или здесь.
Дано:
-Текст, шифрованный правильным ключем.
-Тот же текст, но не зашифрованный.
-Патчинг и брутофорс запрещены и бессмысленны.
В итоге мы должны получить какое-то секретное сообщение.
Необходимый инструментарий: OllyDBG или любой другой отладчик.
Давайте же приступим непосредственно к разбору. Открываем keygenme в Олли и останавливаемся на точке входа.
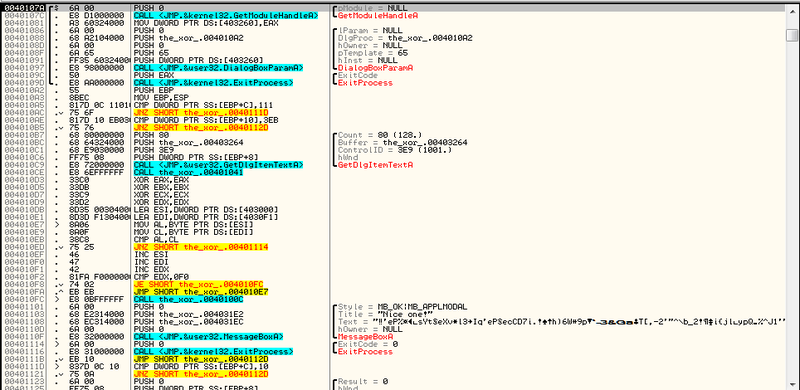
А сейчас необходимо немного осмотреться. Ознакомимся с импортируемыми функциями – благо, в данном файле их не так уж и много. Ставим точки останова на интересующую нас функцию, которая забирает введенный текст из поля – GetDlgItemTextA.
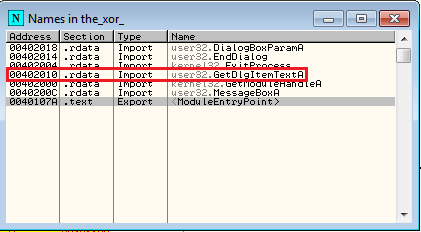
Жмем F9 и перед нами появляется главное окошко пациента. В поле «K E Y» вбиваем все, что душе угодно (я взял слово hello) и жмем ОК.
Далее сработает бряк на нужной нам функции. Нажимаем Ctrl+F9 и останавливаемся на выходе из функции. Сразу после GetDlgItemTextA, которая забирает введенный ключ, следует вызов другой функции. Нажимаем F7 и попадаем в нее.

Продолжаем трассировать, пока не доходим до следующего участка:
CMP EAX,20 ;20h=32d
JNZ SHORT 00401075 ;RETN->ExitProcess
Несколько нажатий F8 и keygenme покидает нас. Что ж, давайте заглянем, куда ведет jnz. Сначала он ведет на команду выхода из функции (RETN), а затем происходит сравнение длины введенного ключа и числа 20h, которые в нашем случае не равны. Потом следует jnz, ведущий на функцию ExitProcess, которая и завершает процесс нашего keygenme.
Хорошо, перезапустим keygenme и введем произвольную строку из 32 символов, я взял такую — 12345678901234567890123456789012. На этот раз мы успешно проходим сравнение и входим в новую функцию.
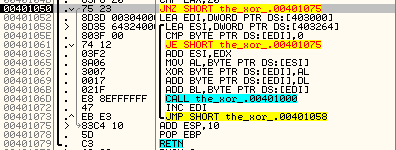
А здесь и происходит чуть ли не самые важные действия во всем keygenme. В EDI перемещается заранее приготовленный незашифрованный текст, а в ESI – введенный ключ.
Затем к ESI прибавляется значение EDX. Зачем это сделано, я расскажу немного ниже. Затем один байт длинной строки xor'ится с байтом из ключа. К xor'енному значению прибавляется значение EDX, а потом все это вдобавок прибавляется к значению нижнего регистра BL.
После всех этих ивзращений вызывается функция (CALL 00401000), которая перемещает значение EBX, т.е результат работы предидущей процедуры, в EAX, регистру EBX присваивается значение 20h и EAX делится на EBX. В конце функции EBX обнуляется.
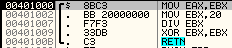
Затем все то же самое происходит со последующими байтами незашифрованного текста из EDI, пока текст не зашифруется. Однако, с ключем все несколько интереснее. Помните, я обещал рассказать, почему к ESI прибавляется EDX? Дело в том, что в регистре EDX хранится остаток деления EAX и EBX из функции 00401000. Этот остаток прибавляется к регистру ESI, который содержит введенный ключ. Значит, остаток является номером байта из введенного нами ключа, который будет xor'ится со следующим байтом из EDI.
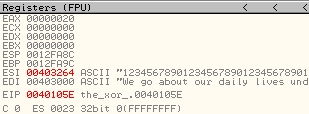
Пример-картинка, показывающая исполнение первого и второго цикла этой функции:

Во время первого цикла EDX = 00000000, поэтому программа использовала первый байт ключа. Во время второго цикла EDX = 00000006, значит программа использовала 7 (1+6) байт ключа.
Ладно, едем дальше. Ставим бряк на выход из процедуры (RETN) по адресу 0x00401079 и нажимаем F9. Останавливаемся на выходе из процедуры с уже шифрованным текстом.
Далее мы видим такую картину:
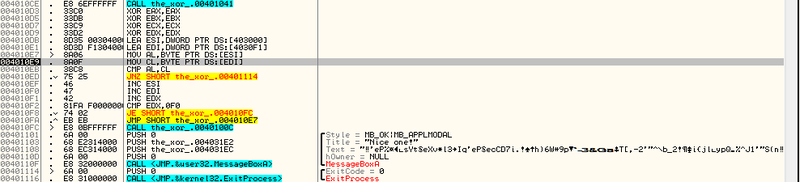
После выхода из главной процедуры очищаются регистры EAX, EBX, ECX и EDX. В ESI помещается строка, зашифрованная с помощью нашего неверного ключа, а в EDI помещается та же строка, только зашифрованная с правильным ключем. Затем в подрегистр AL помещается байт из ESI, в подрегистр СL соответственно помещается байт из EDI. Далее происходит сравнение байтов из CL и AL, и если они равны, то нас отправляют на процедуру расшифровки сообщения (Скажу по секрету, что там происходит то же самое, что и в главной процедуре, только xor'ятся правильный ключ и зашифрованное сообщение). Но т.к. в нашем случае данные подрегистры не равны, отлаживаемый процесс вылетает.
Теперь разберемся, как же генерируется серийник. Псевдоуравнение:
Байт правильно зашифрованного текста = (Байт незашифрованногог текста) xor ((байт ключа[предыдущий байт mod 20h]) + (предыдущий байт ключа mod 32)).
Давайте обозначим все это через переменные для лучшей читаемости и понимания:
Байт незашифрованного текста= s
Байт ключа = х
Предыдущий правильно зашифрованный байт mod 20h = y
Новое уравнение:
Байт правильно зашифрованного текста = s xor (x[y] + y)
Т.к. нас интересует x[y], давайте выразим его через другие переменные:
x[y] = s xor (Байт правильно зашифрованного текста– y)
Для примера вычислим пару первых байтов:
x[1] = 57 xor (3 — 0) = 54h. Смотрим в таблицу ASCII, это знак «T»
y = 3 mod 20 = 3
x[1+3] = 65 xor (50 – 3) = 28h. А это уже знак "(".
И так далее, пока все 32 элемента строки не будут заполнены.
Что ж, теперь можно и свой кейген написать. Предлагаю ознакомиться с моим решением (сорри за Delphi, но это было быстрее всего). Вы можете скачать исполняемый файл отсюда, а исходники посмотреть здесь.
Итак, в последний раз открываем многострадальную тушку нашего подопытного кролика, копируем ключ из кейгена, нажимаем кнопку ОК, созерцаем MessageBox с поздравлениями, радуемся.
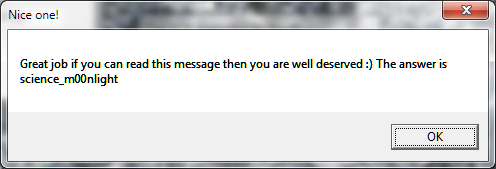
Вот и все. Спасибо за прочтение, надеюсь, это было достаточно весело и познавательно.
Автор: Bernd