Предисловие
На написание статьи меня сподвигло практически полное отсутствие материалов на русском языке про алгоритмы генерации лабиринтов. На Хабре, из того, что вообще есть по теме, можно отметить две статьи: раз и два. Ценность и пользу из которых несет лишь вторая. В первой – просто перевод формального алгоритма и небольшое его пояснение. Что, конечно, неплохо, но очень скудно и не вызывает желания изучать тему дальше.
Если моя статья Вам понравится, я продолжу писать о различных алгоритмах. Мы рассмотрим два самых примитивных и простых случая – генерация двоичного дерева и Сайдвиндер, который, по своей сути, просто чуть измененная версия двоичного дерева со одним заметным плюсом. ОСТОРОЖНО ТРАФИК.
Дам один совет – не подглядывайте в код до тех пор, пока вы не напишите свою реализацию. Вы получите гораздо больше удовольствия и пользы от исправления багов и поиска ошибок, чем если просто переведете с одного языка на другой.
Серьезно. Прислушайтесь к совету. Вы, верно, потратите больше времени, но оно стоит стоит. У меня, например, из-за пары ошибок появился очень забавный генератор «инопланетных» текстов, который можно использовать в различных Sci-Fi играх для создания текста. Надеюсь, Вы изучаете тему для себя и никуда не спешите.
P.S.:
Я буду использовать термин «смещение», предполагая английский bias. Т.е. пристрастие алгоритма к направленности в какую-либо сторону. Например, правое смещение – алгоритм генерирует лабиринты с длинными правыми проходами.
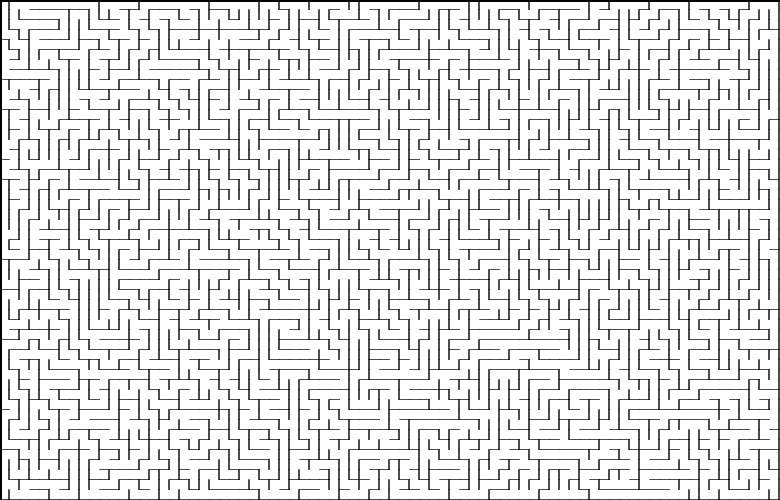
Раскраска лабиринтов происходит относительно расстояния от крайнего левого угла поля до некоторой клетки. Чем дальше от начальной координаты – тем темнее будет цвет.
Идеальный лабиринт – такой лабиринт, в котором одна клетка связана с другой одним единственным путем. Иначе говоря, остовное дерево.
Не стоит переживать, если Вы с Луа незнакомы. Незнание языка никак не помешает Вам понять реализацию, благодаря простоте синтаксиса. Если Вы хотя бы немного умеете программировать, 80% кода не вызовет у Вас проблем с пониманием. Остальные 20% — language specific, про которые я всегда буду писать вначале статьи, объясняя их работу.
Первое, что мне следует сказать:
Lua имеет лишь одну структуру данных – таблицы – ассоциативный массив, при помощи которого мы создаем нужные нам структуры. К примеру, классы, множества, обычные массивы, стаки, очереди и тому подобное. Обращаться к ним мы может либо с помощью строчных-ключей, либо с помощью индексов.
Так же, таблицы не ограничивают нас в хранении только одного типа данных в одном объекте и работают подобно структурам в C/C++. Такой код абсолютно корректен:
ourStructure = {}
ourStructure[“BeautyKey”] = 42
ourStructure[42] = “UltimateAnswer”
ourStructure[1] = falseПрисваивание nil удалит поле:
ourStructure[42] = nilВторое:
Lua не имеет скрытого механизма копирования таблиц. Код, приведенный ниже, не будет копировать и создавать нового объекта SomeNewArray, он лишь скопирует в него ссылку на объект SomeArray, и, следовательно, будет изменять его точно так же, как если Вы передадите значение через неконстантную ссылку или указатель в C/C++:
someArray = {}
someArray[1] = 42
someArray[2] = “ReferencesTest”
someNewArray = someArray
someNewArray[1] = “42 Is Gone, Now Only the Garbage-String here”И третье, для тех, кто хорошо знаком с Lua:
Да, я знаю, что в некоторых местах код избыточен. И то, что в некоторых местах всё можно было бы упростить метаметодами тоже. Следует учитывать то, что код писался в первую очередь для того, чтобы разобраться с алгоритмами, а не для использования в реальном проекте. К тому же, отсутствие избытка специфических для языка функций позволяет выкладывать код в том виде, в котором он есть, без нагромождений комментариев.
Алгоритм двоичного дерева


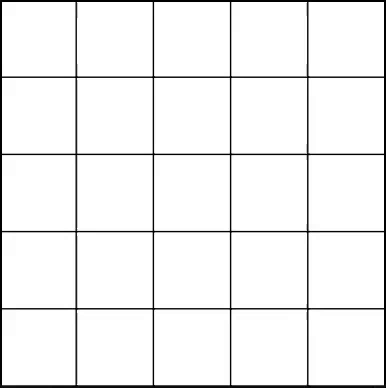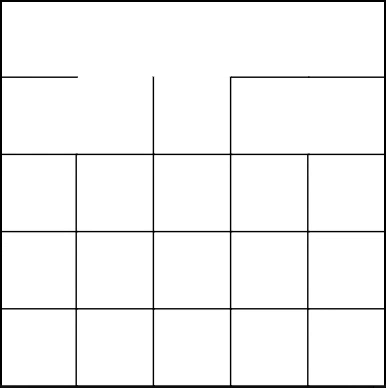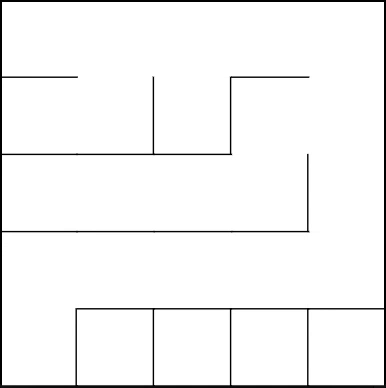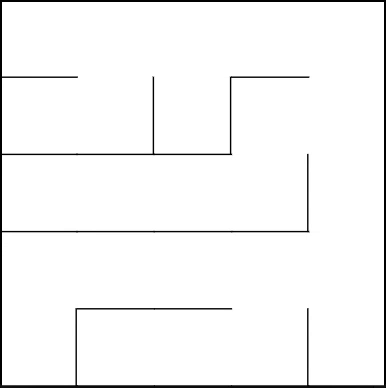

Описание:
Самый первый и самый простой алгоритм в понимании, который я рассмотрю. Его суть заключается в том, чтобы проложить путь в случайном направлении из каждой клетки поля: в моей реализации либо наверх, либо вправо (зависит от выбранного Вами смещения). Мы рассматриваем только 1 клетку за единицу времени, следовательно, мы можем генерировать лабиринты бесконечного размера, сохраняя лишь конечный результат (лабиринт) без необходимости хранить какую-либо побочную информацию.
Такой способ генерации имеет два побочных эффекта:
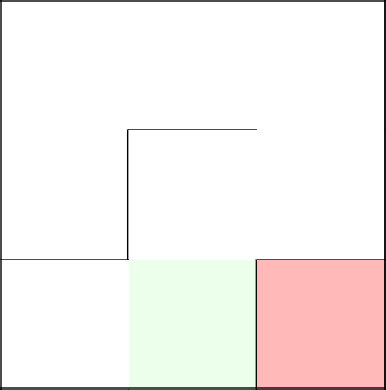
1. Лабиринты обладают сильным диагональным смещением и отсутствием тупиков в его направлении. Посмотрите на скриншоты выше и Вы увидите, что каждый из коридоров стремится к правой верхней клетке, и, как итог, имеет ровно один путь к ней, и нигде на пути нет тупика:
2. Два пустых коридора по сторонам лабиринта. Когда алгоритм «прокапывается» до конца строки/столбца, ему не остается выбора, кроме как продолжить путь в одном единственном направлении, создавая пустые «границы».
К слову, название не просто так совпадает со структурой данных. Результат его работы – случайное двоичное дерево, в котором из каждой клетки (вершины) есть ровно 1 путь по направлению к корню (родительской вершине), и, соответственно, ровно 1 путь к любой другой клетке. Как следствие, любая клетка имеет не более 3 соединений со своими соседями.
Формальный алгоритм (для северо-восточного смещения):
- Выбрать начальную клетку;
- Выбрать случайное направление для прокладывания пути. Если соседняя клетка в этом направлении выходит за границы поля, прокопать клетку в единственно возможном направлении;
- Перейти к следующей клетке;
- Повторять 2-3 до тех пор, пока не будут обработаны все клетки;
Начинаем с координаты (0;0). Наверх в этом ряду пойти не можем, так как иначе выйдем за границы лабиринта. Идем вправо до упора, по пути снося все стены.
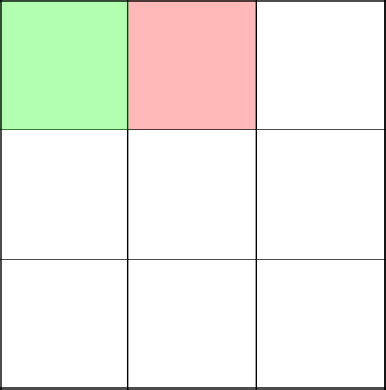
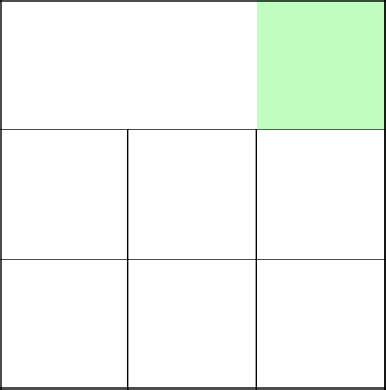
Всё, тупик. Идти некуда. Перемещаемся на следующий ряд и видим, что теперь есть возможность пойти наверх и вправо.

Кидаем монетку и выбираем… Верх. Убираем стену и переходим к следующей клетке.
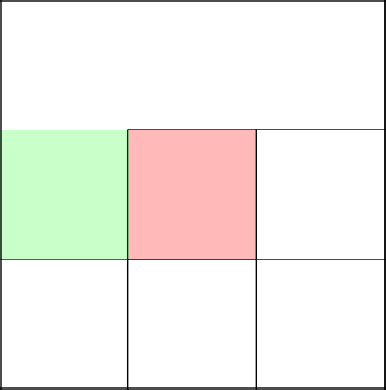
Отлично. Случай подсказывает нам идти направо. Убираем стену и перемещаемся в следующую клетку.

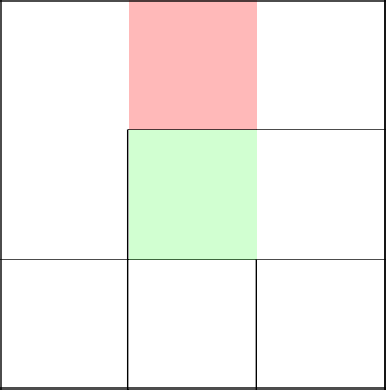

Выбора у нас нет, налево пойти не можем, значит, убираем стену сверху и идем на следующий ряд.

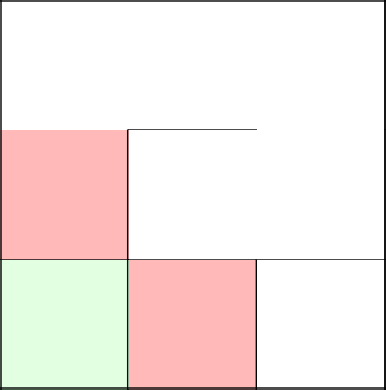
Монета убеждает нас пойти направо. Что же, слушаемся. Убираем стену и переходим к слеудующей клетке.
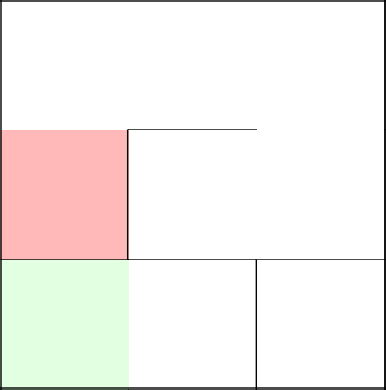
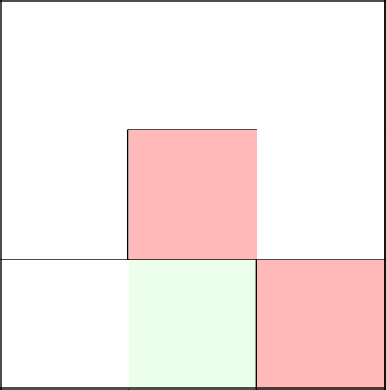
Прокатившись метр, наш несчастный кусок металла падает и говорит, что пора идти наверх. Сносим стену, шагаем к следующей клетке, и, так как она крайняя в этом ряду, убираем стену сверху. Лабиринт закончен.
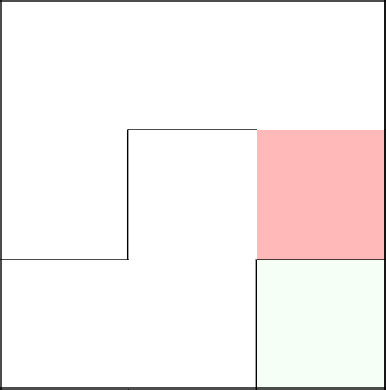

Плюсы:
- Простая реализация;
- Высокая скорость работы;
- Возможность генерировать бесконечные лабиринты;
Минусы:
- Низкая сложность рисунка;
- Сильное смещение по диагонали;
- Отсутствие тупиков по смещению;
- Однообразность сгенерированных лабиринтов;
local mod = {}
local aux = {}
aux.width = false
aux.height = false
aux.sx = false
aux.sy = false
aux.grid = false
function aux.createGrid (rows, columns)
local MazeGrid = {}
for y = 1, rows do
MazeGrid[y] = {}
for x = 1, columns do
MazeGrid[y][x] = {bottom_wall = true, right_wall = true} -- Wall grid
end
end
return MazeGrid
end
-- Binary Tree North-East variant
function mod.createMaze(x1, y1, x2, y2, grid)
aux.width, aux.height, aux.sx, aux.sy = x2, y2, x1, y1
aux.grid = grid or aux.createGrid(aux.height, aux.width)
aux.binarytree()
return aux.grid
end
function aux.binarytree()
for y = aux.sy, aux.height do
for x = aux.sx, aux.width do
if y ~= aux.sy then
if math.random(0, 1) == 0 then
if x ~= aux.width then
aux.grid[y][x].right_wall = false
else
aux.grid[y-1][x].bottom_wall = false
end
else
aux.grid[y-1][x].bottom_wall = false
end
else
if x ~= aux.width then
aux.grid[y][x].right_wall = false
end
end
end
end
end
return mod
Алгоритм «Sidewinder»

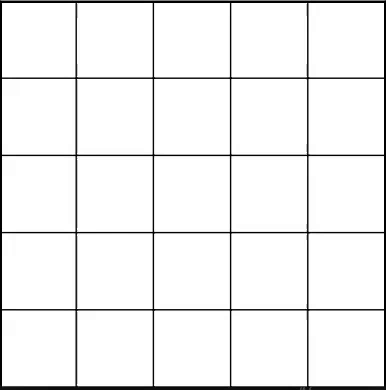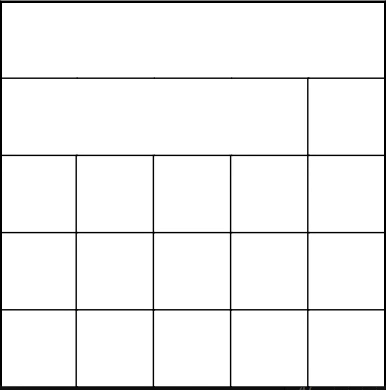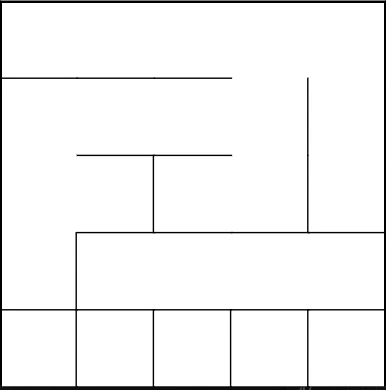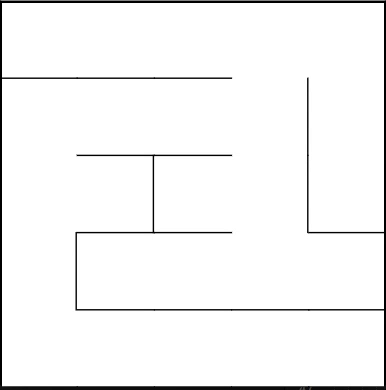

Описание:
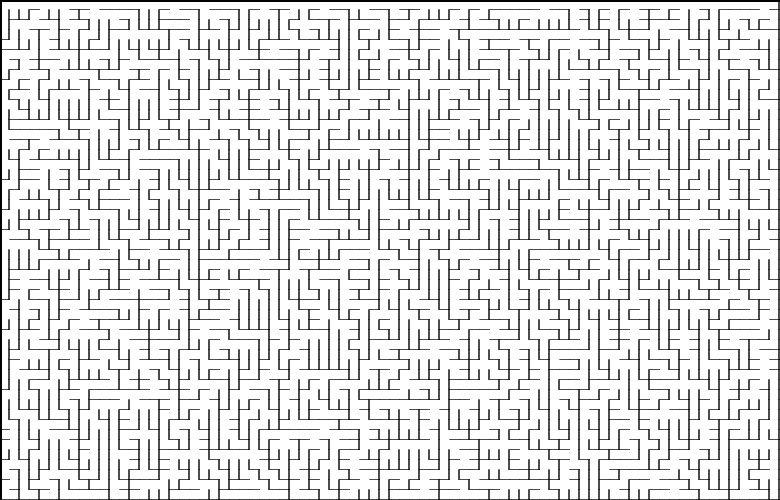
Алгоритм с непереводимым названием Sidewinder по своей работе очень похож на алгоритм двоичного дерева, в том отличии, что в нём нет характерного смещения по диагонали, одного пустого коридора и клетки мы рассматриваем не по отдельности, а множествами. Лабиринты получаются с преимущественно вертикальным или горизонтальным смещением (в зависимости от реализации), с отсутствием тупиков в их направлении. В сравнении со своим более примитивным собратом, смещение не так заметно и больше похоже на «спираль», которая плавно сменяет вертикальные и горизонтальные коридоры.
Немного про побочные эффекты. Sidewinder создает только один пустой коридор на одной стороне, вместо двух. Начиная создание множеств с первого ряда поля, у нас отсутствует возможность прокопать путь наверх, так как мы находимся в самом крайнем вертикальном положении и попытка пойти выше приведет к выходу за границы поля. Но и если мы будем организовывать множества без выхода по вертикали, мы создадим несколько изолированных друг от друга областей.
Для примера: 9 клеток первого ряда можно поделить на три множества, между которыми расположены стены. Каждое множество второго ряда будет прокапывать путь к одному из трех «блоков» выше. Третий ряд проложит путь к «блокам» второго. И так до конца поля. В итоге, у нас получатся 3 разветвленные, изолированные друг от друга вертикальные области, что не подходит для идеального лабиринта, в котором из каждой точки поля есть ровно 1 путь в любую другую.
Формальный алгоритм (для стандартного смещения):
- Выбрать начальный ряд;
- Выбрать начальную клетку ряда и сделать её текущей;
- Инициализировать пустое множество;
- Добавить текущую клетку в множество;
- Решить, прокладывать ли путь направо;
- Если проложили, то перейти к новой клетке и сделать её текущей. Повторить шаги 3-6;
- Если не проложили, выбираем случайную клетку множества и прокладываем оттуда путь наверх. Переходим на следующий ряд и повторяем 2-7;
- Продолжать, пока не будет обработан каждый ряд;
Мы начинаем с первого ряда и видим, что выше нас – выход за пределы поля. Сносим все стены и идем сразу во второй ряд, создаем пустое множество.
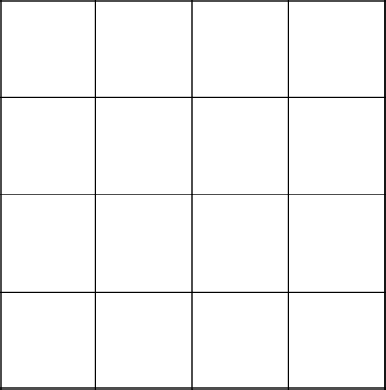
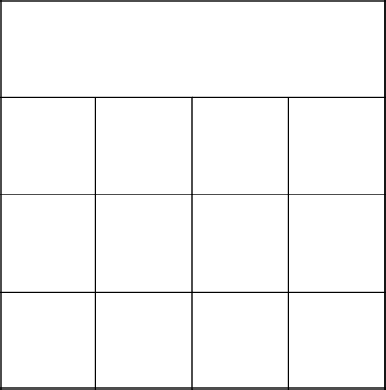
Так, а вот тут интереснее. Давайте добавим в множество первые две клетки ряда.
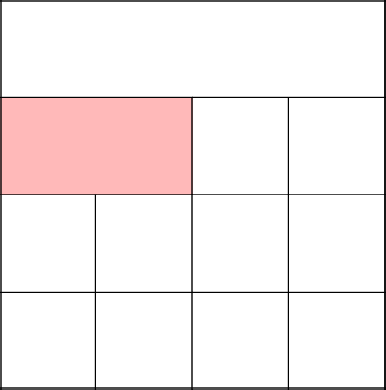
Выбираем одну из этих клеток и убираем относящуюся к ней верхнюю стенку в первый ряд.

Обнуляем множество, добавляем в нее следующую клетку ряда.
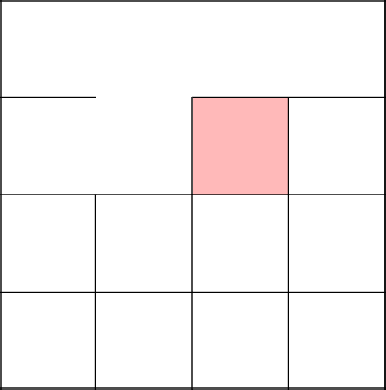
В этот раз ни с кем не объединяем, просто прокладываем путь наверх прямо из этой единственной клетки.

Повторяем наши действия. Обнуляем множество, переходим в следующую клетку, добавляем её… А так как она осталась последней в ряде, то так же убираем стену сверху и идем в ряд ниже.
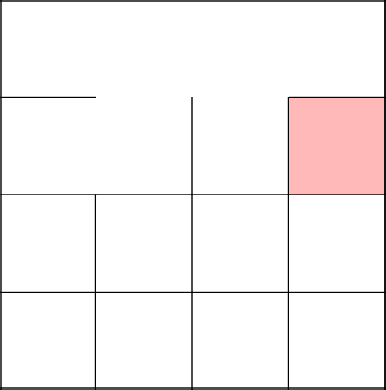

А теперь сразу объединяем три первые клетки в одно множество.
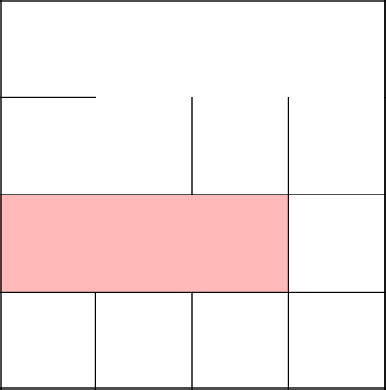
Случайно выбираем клетку, в нашем случае, вторую и убираем стену сверху к предыдущему ряду.

Ну, тут у нас опять нет выбора, убираем стену наверху и идем на ряд ниже.
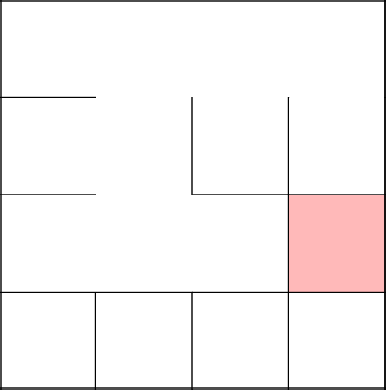

На этот раз, самую перваую клетку мы сделаем единственной. Убираем стену к предыдущему ряду и идем дальше, в следующую клетку.
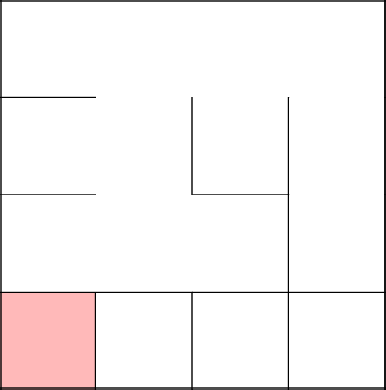

Предположим, что захотели в конце объединить три клетки.
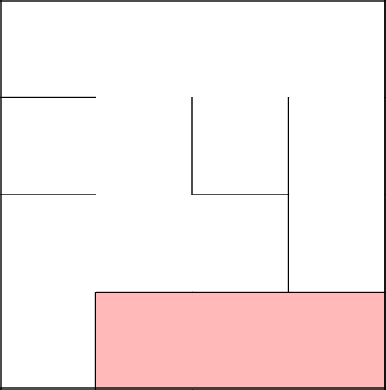
И снова нам приглянулась средняя клетка из множества, из которой и убираем стену наверх. Всё, наш лабиринт готов.

Плюсы:
- Возможность генерировать бесконечные лабиринты;
- Только 1 пустой коридор;
- Более сложный рисунок, в отличии от алгоритма двоичного дерева;
Минусы:
- Более запутанная реализация;
- Отсутствие тупиков по смещению;
- Сильное вертикальное смещение;
local mod = {}
local aux = {}
aux.width = false
aux.height = false
aux.sx = false
aux.sy = false
aux.grid = false
function aux.createGrid (rows, columns)
local MazeGrid = {}
for y = 1, rows do
MazeGrid[y] = {}
for x = 1, columns do
MazeGrid[y][x] = {bottom_wall = true, right_wall = true}
end
end
return MazeGrid
end
function mod.createMaze(x1, y1, x2, y2, grid)
aux.height, aux.width, aux.sx, aux.sy = y2, x2, x1, y1
aux.grid = grid or aux.createGrid(y2, x2)
aux.sidewinder()
return aux.grid
end
function aux.sidewinder()
local cx = aux.sx --[[ cx – координата начала множества по x. У нас нет надобности создавать отдельный массив для сета, так как его элементы всегда располагаются строго в ряд ]]
for y = aux.sy, aux.height do
for x = aux.sx, aux.width do
if y ~= aux.sy then
if math.random(0, 1) == 0 and x ~= aux.width then
aux.grid[y][x].right_wall = false
else
aux.grid[y-1][math.random(cx, x)].bottom_wall = false
if x ~= aux.width then
cx = x+1
else
cx = aux.sx
end
end
else
if x ~= aux.width then
aux.grid[y][x].right_wall = false
end
end
end
end
end
return mod
Эпилог
Надеюсь, Вам понравилась статья и Вы почерпнули новые знания о примитивной процедурной генерации лабиринтов. Я выбрал два самых простых в реализации и работе алгоритма, чтобы новичкам было проще «пощупать» тему и понять, хотят ли они изучать её дальше. Мне важно знать, интересны ли такие статьи людям на Хабрахабре и стоит ли продолжать их писать. Для читателей у меня есть еще минимум 9 классических алгоритмов, которые стоит рассмотреть. Какие-то представляют из себя случайное блуждание по полю, как, например, алгоритм Прима или Уилсона, какие-то требуют больше ресурсов для работы, так как работают с графами, например, Эллер и Крускал, а какие-то выдерживают золотую середину. Но и это не конец – у меня в рукаве есть такие вещи, как: полярные (круглые) лабиринты, генерация лабиринтов на различной сетке (гексы, треугольник и пр.), маскинг лабиринтов в надписи и формы, 2.5Д лабиринты и 3Д, теория лабиринтов, статистическое сравнение алгоритмов, комбинированные алгоритмы генерации. В конце концов, у нас есть еще огромное множество вариаций типов лабиринтов. Например, сейчас мы рассматриваем идеальные алгоритмы, в которых из каждой точки есть ровно один путь в любую другую. Но ведь есть еще и те, которые позволяют одной клетке иметь несколько путей для любой другой! Например, Quake, Doom и прочие шутеры в только-только зарождающемся жанре использовали такие алгоритмы для генерации уровней, по некоторым слухам.
Поэтому, если Вам понравилась статья, тема, и Вы хотите видеть их дальше – то, пожалуйста, напишите об этом в комментарии. Так же, буду очень рад любой критике, как в техническом плане, так и в лингвистическом и стилистическом.
Автор: RussDragon






