FDTD (Finite Difference Time Domain) — метод конечных разностей во временной области — самый «честный» метод решения задача электродинамики от низких частот до видимого диапазона. Суть — решение уравнений Максвелла «в лоб». Здесь неплохо расписано. Особенно посмотрите сетку.
Задача решалась в двумерном случае простой явной разностной схемой. Неявные схемы я не люблю, и они требуют много памяти. Расчет с нормальной точностью требует сеток малого шага, по сравнению с более простыми методами требуется очень много времени. Поэтому максимальный упор был сделан на производительность.
Представлена реализация алгоритма на Java и C++.

Предисловие
Около шести лет основным моим языком для расчетов и мелочей был Matlab. Причина — простота написания и визуализации результата. А так как перешел я с Borland C++ 3.1, то прогресс возможностей был очевиден. (В Python я никогда не шарил, а в С++ тогда слабо).
FDTD нужен был мне для расчетов как надежный и достоверный метод. Начал изучать вопрос в 2010–11 годах. Имеющиеся пакеты или было непонятно, как использовать, или не умели то, что мне нужно. Решил написать свою программу для четкого контроля над всем. Прочитав классическую статью «Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media», написал трехмерный случай, но потом упростил его до двумерного. Почему 3D — это сложно, объясню потом.
Потом максимально оптимизировал и упрощал код Matlab. После всех улучшений получилось, что сетка 2000х2000 проходится за 107 минут. На i5-3.8 ГГц. Тогда такой скорости хватало. Из полезного было то, что в Матлабе сразу шел расчет комплексных полей, и легко было показывать картинки распространения. Также все считалось на даблах, потому что на скорость Матлаба практически не влияло. Да, стандартный мой расчет — один проход света по фотонному кристаллу.
Проблемы было две. Понадобилось с высокой точностью вычислять спектры, а для этого использовать большую ширину сетки. А физическое увеличение области по обеим координатам в 2 раза увеличивает время расчета в 8 раз (размер кристалла*время прохода).
Matlab я продолжал использовать, но стал Java-программистом. И, сравнивая производительность разных алгоритмов, начал что-то подозревать. К примеру, сортировка пузырьком — только циклы, массивы и сравнения — в Матлабе работает в 6 раз медленнее, чем в С++ или Java. И этого для него еще хорошо. Пятимерный цикл для гипотезы Эйлера в Матлабе раз в 400 дольше.
Вначале принялся писать FDTD на C++. Там был встроенный std::complex. Но тогда я забросил эту идею. (В Матлабе не такие скобочки, копипаст не работал, пришлось потратить каплю времени) Сейчас проверил C++ — комплексная математика дает потери скорости в 5 раз. Это слишком много. В результате написал на Java.
Немного о вопросе «Почему на Java?». Детали производительности опишу потом. Если коротко — на простом не ООП коде, только арифметика и циклы — C++ с оптимизацией О3 или такой же скорости, или до +30% быстрее. Просто сейчас я лучше разбираюсь в Java, интерфейсе и работе с графикой.
FDTD – детальнее
Теперь перейдем к коду. Попытаюсь показать все, с объяснениями задачи и алгоритма. В двумерном случае система уравнений Максвелла распадается на две независимых подсистемы — ТЕ и ТМ волны. Код показан для ТЕ. Имеются 3 компоненты — электрическое поле Ez и магнитные Hx, Hy. Для упрощения время имеет размерность метров.
Изначально я думал, что от float смысла нет, так как все вычисления приводятся к double. Поэтому приведу код для double — в нем меньше лишнего. Все массивы имеют размеры +1, чтоб индексы совпадали с матрицами Матлаба (от 1, а не от 0).
Где-то в начальном коде:
public static int nx = 4096;// ширина области. Степень 2 для Фурье.
public static int ny = 500;// длина областиОсновной метод:
public static double[][] callFDTD(int nx, int ny, String method) {
int i, j;// индексы для циклов
double x; //метрическая координата
final double lambd = 1064e-9; // Длина волны в метрах
final double dx = lambd / 15; // размер шага сетки. Максимум λ/10. Чем меньше, тем выше точность.
final double dy = dx; //реально в коде не используется. Ячейки квадратные
final double period = 2e-6; // поперечный период решетки фотонного кристалла
final double Q = 1.0;// специфическое отношение
final double n = 1;// минимальный показатель преломления кристалла
final double prodol = 2 * n * period * period / lambd / Q; //продольный период
final double omega = 2 * PI / lambd; // циклическая частота световой волны
final double dt = dx / 2; // шаг по времени. НЕ больше, чем по координате
final double tau = 2e-5 * 999;// время затухания источника света. Нужно для запуска коротких импульсов. Если большое, затухание незаметно.
final double s = dt / dx; //отношение шага по времени и пространству
final double k3 = (1 - s) / (1 + s);// для граничных условий
final double w = 19e-7;// полуширина гауссова пучка
final double alpha = sin(0.0 / 180 * PI);// угол лазерного пучка от нормали. В радианах.
double[][] Ez = new double[nx + 1][ny + 1];
double[][] Hx = new double[nx][ny]; // основные массивы полей
double[][] Hy = new double[nx][ny];
final int begin = 10; // координата, где пустота сменяется кристаллом. Без необходимости много не ставить.
final double mod = 0.008 * 2;//максимальная глубина модуляции диэлектрической проницаемости = 2*Δn;
final double ds = dt * dt / dx / dx;// константа для подгона систем исчисленияИнициализация диэлектрической проницаемости (решетка кристалла). Точнее, обратная величина с константами. Используется дискретная функция (0 или 1). Это мне кажется ближе к реальным образцам. Конечно, сюда можно написать что угодно:
double[][] e = new double[nx + 1][ny + 1];
for (i = 1; i < nx + 1; i++) {
for (j = 1; j < ny + 1; j++) {
e[i][j] = ds / (n + ((j < begin) ? 0 : (mod / 2) * (1 + signum(-0.1 + cos(2 * PI * (i - nx / 2.0 + 0.5) * dx / period) * sin(2 * PI * (j - begin) * dy / prodol)))));
}
}Решетка кристалла выглядит примерно так:

Массивы, используемые для граничных условий:
double[][] end = new double[2][nx + 1];
double[][] top = new double[2][ny + 1];
double[][] bottom = new double[2][ny + 1];Предел счета по времени. Поскольку у нас шаг dt = dx / 2, стандартный коэффициент 2. Если среда плотная, или нужно идти под углом — больше.
final int tmax = (int) (ny * 2.2);Начинаем главный цикл:
for (int t = 1; t <= tMax; t++) {
double tt = Math.min(t * s + 10, ny - 1);Переменная tt тут учитывает ограничение скорости света, с небольшим запасом. Мы будем считать только ту область, куда свет мог дойти.
Вместо комплексных чисел я считаю отдельно две компоненты — синус и косинус. Я подумал, что для скорости лучше скопировать кусок, чем делать выбор внутри цикла. Возможно, заменю на вызов функции или лямбду.
switch (method) {
case "cos":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5); // поперечная координата в метрах
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * cos((x * alpha + (t - 1) * dt) * omega);
}
break;case "sin":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5);
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * sin((x * alpha + (t - 1) * dt) * omega);
}
break;
}
Тут у нас на вход области (в крайнюю левую координату) поступает гауссов луч полуширины w, под углом alpha, осцилирующий во времени. Именно так и возникает «лазерное» излучение нужной нам частоты/длины волны.
Дальше копируем временные массивы под поглощающие граничные условия Мура:
for (i = 1; i <= nx; i++) {
end[0][i] = Ez[i][ny - 1];
end[1][i] = Ez[i][ny];
}
System.arraycopy(Ez[1], 0, top[0], 0, ny + 1);
System.arraycopy(Ez[2], 0, top[1], 0, ny + 1);
System.arraycopy(Ez[nx - 1], 0, bottom[0], 0, ny + 1);
System.arraycopy(Ez[nx], 0, bottom[1], 0, ny + 1);Теперь переходим к главному вычислению — следующему шагу по полю. Особенность уравнений Максвелла — изменение во времени магнитного поля зависит только от электрического, и наоборот. Это позволяет написать простую разностную схему. Исходные формулы были такие:
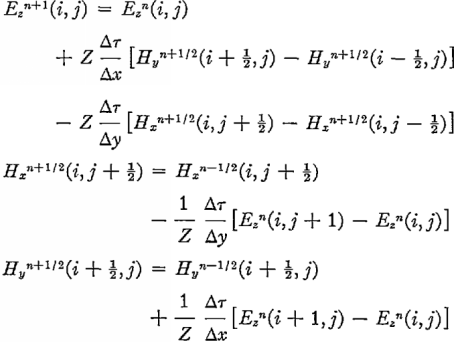
Все лишние константы я пересчитал заранее, заменил размерность Н, внес и учел диэлектрическую проницаемость. Поскольку оригинальные формулы для сетки, сдвинутой на 0,5, нужно не ошибиться с индексами массивов Е и Н. они разной длины — Е на 1 больше.
Цикл по области для Е:
for (i = 2; i <= nx - 1; i++) {
for (j = 2; j <= tt; j++) {//можно ли тут оптимизировать порядок доступа к ячейкам?
Ez[i][j] += e[i][j] * ((Hx[i][j - 1] - Hx[i][j] + Hy[i][j] - Hy[i - 1][j]));
}
}А теперь наконец-то применяем граничные условия. Они нужны потому, что разностная схема не считает крайние ячейки — для них нет формул. Если ничего не делать, свет будет отражаться от стенок. Поэтому применяем метод, минимизирующий отражение при нормальном падении. Обрабатываем три стороны — верх, низ и право. Потери производительности на граничные условия около 1% (тем меньше, чем больше задача).
for (i = 1; i <= nx; i++) {
Ez[i][ny] = end[0][i] + k3 * (end[1][i] - Ez[i][ny - 1]);//end
}
for (i = 1; i <= ny; i++) {
Ez[1][i] = top[1][i] + k3 * (top[0][i] - Ez[2][i]);//verh kray
Ez[nx][i] = bottom[0][i] + k3 * (bottom[1][i] - Ez[nx - 1][i]);
}Слева граница особая — в ней генерится луч. Также, как в прошлый раз. Просто на 1 шаг дальше по времени.
switch (method) {
case "cos":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5);
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * cos((x * alpha + t * dt) * omega);
}
break;
case "sin":
for (i = 1; i <= nx - 1; i++) {
x = dx * (i - (double) nx / 2 + 0.5);
Ez[i][1] = exp(-pow(x, 2) / w / w - (t - 1) * dt / tau) * sin((x * alpha + t * dt) * omega);
}
break;
}
Осталось только посчитать магнитное поле:
for (i = 1; i <= nx - 1; i++) { // main Hx Hy
for (j = 1; j <= tt; j++) {
Hx[i][j] += Ez[i][j] - Ez[i][j + 1];
Hy[i][j] += Ez[i + 1][j] - Ez[i][j];
}
}
} // конец 3-мерного цикла.И еще мелочи: передать конечный отрезок для вычисления преобразования Фурье — нахождения картины в дальней зоне (пространство направлений):
int pos = method.equals("cos") ? 0 : 1; //какую из компонент записывать
BasicEx.forFurier[pos] = new double[nx]; //там в коде массив для Фурье
int endF = (int) (ny * 0.95);// произвольная координата в конце
for (i = 1; i <= nx; i++) {
BasicEx.forFurier[pos][i - 1] = Ez[i][endF];
for (j = 1; j <= ny; j++) {
Ez[i][j] = abs(Ez[i][j]);// ABS
} //я вот сейчас понял, что брать модуль не надо - я потом беру квадарат
}
Hx = null; //я верю, что это очистит память
Hy = null;
e = null;
return Ez;
} for (int i = 0; i < nx + 1; i++) {
for (int j = 0; j < ny + 1; j++) {
co.E[i][j] = co.E[i][j] * co.E[i][j] + si.E[i][j] * si.E[i][j];
}
}
Отдельно берем преобразование Фурье:
fft.fft(forFurier[0], forFurier[1]);Поскольку в быстром Фурье не разбираюсь, взял первый попавшийся. Минус — ширина только степень двойки.
О производительности
Переходим к самому интересному для меня — что хорошего мы получили, перейдя с Матлаба на Java. В Матлабе я в свое время оптимизировал все, что смог. В Java — в основном внутренний цикл (сложность n^3). У Матлаба уже учтено то, что он считает сразу две компоненты. Скорость на первом этапе (больше — лучше):
| Matlab | 1 |
| Java double | 50 |
| C++ gcc double | 48 |
| C++ MSVS double | 55 |
| C++ gcc float | 73 |
| C++ MSVS float | 79 |
Опишем основных участников состязания.
- Matlab — 2011b и 2014. Переход на 32-битные числа дает очень малый прирост скорости.
- Java — вначале 7u79, но в основном 8u102. Мне показалось, что 8 немного лучше, но детально не сравнил.
- Microsoft VisualStudio 2015 конфигурация release
- MinGW gcc — фиг знает какой, декабрь 2014, всегда оптимизация O3. Оптимизация под Core i, без AVX. AVX у меня на ноуте нет, там где есть прироста не давал.
- Pentium 2020m 2.4 GHz, ddr3-1600 1 канал
- Core i5-4670 3.6–3.8 GHz, ddr3-1600 2 канала
- Core i7-4771 3.7–3.9 GHz, ddr3-1333 2 канала
- Athlon x3 3.1 GHz, ddr3-1333, очень медленный контролер памяти.
2-ядерный этап
Вначале я считал ТЕ и ТМ компоненты последовательно. Кстати, это единственный вариант при нехватке памяти. Потом написал два потока — простые Runnable. Вот только прогресса была мало. Всего на 20-22% быстрее, чем 1-поточное. Начал искать причины. Потоки работали нормально. 2 ядра стабильно грузились на 100%, не давая жить ноуту.
Потом я посчитал производительность. Получилось, что она упирается в скорость оперативной памяти. Код уже работал на пределе чтения. «Пришлось» переходить на float. Проверка точности показала, что никаких смертельных погрешностей нет. Визуальной разницы однозначно нет. Суммарная энергия отличалась в 8 знаке. После интегрального преобразования максимум спектра — на 0,7e-6.
Но главное — получил рывок производительности. Общий эффект от 2 ядер и перехода на float +87–102%. (Чем быстрее память и больше ядер, тем лучше прирост). Athlon x3 дал мало прироста.
Реализация на С++ аналогичная — через std::thread (смотри в конце).
Текущие скорости (2 threads):
| Java double | 61 |
| Java float | 93-101 |
| C++ gcc float | 99-110 |
Все оценки проводились для однократного запуска расчета. Потому-что, если повторно запускать из GUI, не закрывая программу, дальше скорость возрастает. Имхо, jit-оптимизация рулит.
4-ядерный этап
Мне казалось, что еще есть куда ускоряться. Я принялся за 4-поточный вариант. Суть — область делится пополам и считается в 2 потоках, вначале по Е, потом по Н.
Вначале написал его на Runnable. Получилось ужасно — ускорение было только для очень большой ширины области. Слишком большие затраты на порождение новых потоков. Потом освоил java.util.concurrent. Теперь у меня был фиксированный пул потоков, которым давались задания:
public static ExecutorService service = Executors.newFixedThreadPool(4);
//……
cdl = new CountDownLatch(2);
NewThreadE first = new NewThreadE(Ez, Hx, Hy, e, 2, nx / 2, tt, cdl);
NewThreadE second = new NewThreadE(Ez, Hx, Hy, e, nx / 2 + 1, nx - 1, tt, cdl);
service.execute(first);
service.execute(second);
try {
cdl.await();
} catch (InterruptedException ex) {
} cdl = new CountDownLatch(2);
NewThreadH firstH = new NewThreadH(Ez, Hx, Hy, 1, nx / 2, tt, cdl);
NewThreadH secondH = new NewThreadH(Ez, Hx, Hy, nx/2+1, nx-1, tt, cdl);
service.execute(firstH);
service.execute(secondH);
try {
cdl.await();
} catch (InterruptedException ex) {
}
Внутри потока выполняются пол цикла.
public class NewThreadE implements Runnable {
float[][] Ez;
float[][] Hx;
float[][] Hy;
float[][] e;
int iBegin;
int iEnd;
float tt;
CountDownLatch cdl;
public NewThreadE(float[][] E, float[][] H, float[][] H2, float[][] eps,
int iBegi, int iEn, float ttt, CountDownLatch cdl) {
this.cdl = cdl;
Ez = E;
Hx = H;
Hy = H2;
e = eps;
iBegin = iBegi;
iEnd = iEn;
tt = ttt;
}
@Override
public void run() {
for (int i = iBegin; i <= iEnd; i++) { // main Ez
for (int j = 2; j <= tt; j++) {
Ez[i][j] += e[i][j] * ((Hx[i][j - 1] - Hx[i][j] + Hy[i][j] - Hy[i - 1][j]));
}
}
cdl.countDown();
}
}
Аналогичный класс для Н — просто другие границы и свой цикл.
Теперь прирост от 4 потоков есть всегда — от 23 до 49% (.jar). Чем меньше ширина, тем лучше — судя по скорости, мы влезаем в кеш-память. Наибольшая польза будет, если считать длинные узкие задачи.
| Java float 4потока | 124–151 |
| C++ gcc float 4потока | 115–162 |
Реализация на С++ пока содержит только простые std::thread. Поэтому для нее чем шире, тем лучше. Ускорение С++ от 5% при ширине 1024 до 47% на 16384.
Как мы видим, в самом лучшем случае прирост 49% — как почти 3 ядра. Поэтому имеем забавный факт — при малых задачах лучше всего ставить newFixedThreadPool(3);
Для больших — по количеству потоков в процессоре — 4 или 6-8. Укажу еще забавный факт. На Атлоне х3 был очень слабый прогресс от перехода на float и 2 потоков — 32% от обеих оптимизаций. Прирост от «4»-ядерного кода на С++ также невелик — 67% между 1 и 4 ядрами (оба float). Списывать можно на медленный контролер памяти и 32-битную Винду.
Но 4-ядерный Java-код отработал отлично. При 3 потоках Екзекутора +50,2% от 2-ядерной версии для больших задач. Почему-то худшая 2-ядерная реализация усилилась максимально возможной многоядерной.
Последнее замечание по 4-ядерному коду в Java. Текущие затраты времени:
| Основные 2-мерные циклы Е и Н | 83% |
| Прочее, считая начальную инициализацию всего | 16% |
| Порождение (4) потоков | Около 1% (0,86 по профилировщику) |
Я постарался максимально оптимизировать основные циклы, думая что остальное тратит мало времени.
Выкладываю также полный код 4-ядерного случая на С++:
#include <iostream>
#include <complex>
#include <stdio.h>
#include <sys/time.h>
#include <thread>
using namespace std;
void thE (float** &Ez, float** &Hx, float** &Hy, float** &e,
int iBegin, int iEnd, float tt)
{
for (int i = iBegin; i <= iEnd; i++) // main Ez
{
for (int j = 2; j <= tt; j++)
{
Ez[i][j] += e[i][j] * ((Hx[i][j - 1] - Hx[i][j] + Hy[i][j] - Hy[i - 1][j]));
}
}
}
void thH (float** &Ez, float** &Hx, float** &Hy,
int iBegin, int iEnd, float tt)
{
for (int i = iBegin; i <= iEnd; i++)
{
for (int j = 1; j <= tt; j++)
{
Hx[i][j] += Ez[i][j] - Ez[i][j + 1];
Hy[i][j] += Ez[i + 1][j] - Ez[i][j];
}
}
}
void FDTDmainFunction (char m)
{
//m=c: cos, else sin
int i,j;
float x;
const float dx=0.5*1e-7/1.4;
const float dy=dx;
const float period=1.2e-6;
const float Q=1.5;
const float n=1;//ne используется в Эпсилон матрице пока =1
const float lambd=1064e-9;
const float prodol=2*n*period*period/lambd/Q;
const int nx=1024;
const int ny=700;
float **Ez = new float *[nx+1];
for (i = 0; i < nx+1; i++)
{
Ez[i] = new float [ny+1];
for (j=0; j<ny+1; j++)
{
Ez[i][j]=0;
}
}
float **Hx = new float *[nx];
for (i = 0; i < nx; i++)
{
Hx[i] = new float [ny];
for (j=0; j<ny; j++)
{
Hx[i][j]=0;
}
}
float **Hy = new float *[nx];
for (i = 0; i < nx; i++)
{
Hy[i] = new float [ny];
for (j=0; j<ny; j++)
{
Hy[i][j]=0;
}
}
const float omega=2*3.14159265359/lambd;
const float dt=dx/2;
const float s=dt/dx;//for MUR
const float w=40e-7;
const float alpha =tan(15.0/180*3.1416);
float** e = new float *[nx+1];
for (i = 0; i < nx+1; i++)
{
e[i] = new float [ny+1];
for (j=0; j<ny+1; j++)
{
e[i][j]=dt*dt / dx/dx/1;
}
}
const int tmax= (int) ny*1.9;
for (int t=1; t<=tmax; t++)
{
float tt=min(t*s+10,(float)(ny-1));
if (m == 'c')
{
for (i=1; i<=nx-1; i++)
{
x = dx*(i-(float)nx/2+0.5);
Ez[i][1]=exp(-pow(x,2)/w/w)*cos((x*alpha+(t-1)*dt)*omega);
}
}
else
{
for (i=1; i<=nx-1; i++)
{
x = dx*(i-(float)nx/2+0.5);
Ez[i][1]=exp(-pow(x,2)/w/w)*sin((x*alpha+(t-1)*dt)*omega);
}
}
std::thread thr01(thE, std::ref(Ez), std::ref(Hx), std::ref(Hy), std::ref(e), 2, nx / 2, tt);
std::thread thr02(thE, std::ref(Ez), std::ref(Hx), std::ref(Hy), std::ref(e), nx / 2 + 1, nx - 1, tt);
thr01.join();
thr02.join();
// H
for (i=1; i<=nx-1; i++)
{
x = dx*(i-(float)nx/2+0.5);
Ez[i][1]=exp(-pow(x,2)/w/w)*cos((x*alpha+t*dt)*omega);
}
std::thread thr03(thH, std::ref(Ez), std::ref(Hx), std::ref(Hy), 1, nx / 2, tt);
std::thread thr04(thH, std::ref(Ez), std::ref(Hx), std::ref(Hy), nx / 2 + 1, nx - 1, tt);
thr03.join();
thr04.join();
}
}
int main()
{
struct timeval tp;
gettimeofday(&tp, NULL);
double ms = tp.tv_sec * 1000 + (double)tp.tv_usec / 1000;
std::thread thr1(FDTDmainFunction, 'c');
std::thread thr2(FDTDmainFunction, 's');
thr1.join();
thr2.join();
gettimeofday(&tp, NULL);
double ms2 = tp.tv_sec * 1000 + (double)tp.tv_usec / 1000;
cout << ms2-ms << endl;
return 0;
}Это самый простой код, без нормальной решетки и граничных условий. Интересно, можно ли в С++ эффективнее объявлять 2-мерные массивы и вызывать потоки?
8 ядер
А больше ядер у меня нет. Если бы мои задачи не упирались в память, делил бы дальше. Вроде, ThreadPool дает малые затраты. Или переходить на Fork-Join Framework.
Я мог бы проверить — отказаться от первых двух потоков, и делить одну задачу на 4-8 кусков на i7. Но смысл будет, только если кто-то протестирует на машине с быстрой памятью — DDR-4 или 4 канала.
Лучший способ избавиться от нехватки скорости памяти — видеокарты. Переходить на Cuda мне мешает брат, который запрещает обновлять видеодрайвер (незнание С и Cuda).
Итог и послесловия
Я могу быстро решить любую нужную мне 2-мерную задачу с хорошей точностью. Сетка 4096х2000 проходится на 4-ядернике за 106 секунд. Это будет 300 микрон х 40 слоев — максимальные образцы у нас.
В 2D при 32-битной точности требуется немного памяти — 4байта*4массива*2 комплексных компоненты = 32 байта / пиксель в худшем случае.
В 3D все намного хуже. Компонент уже шесть. Можно отказаться от двух потоков — считать компоненты последовательно и писать на винт. Можно не хранить массив диэлектрической проницаемости, а считать в цикле или обойтись очень маленьким периодическим участком. Тогда в 16 ГБ оперативы (максимум у меня на работе) влезет область 895х895х895. Это будет нормально «чтоб посмотреть». Зато считаться будет «всего» 6–7 часов один проход. Если задачу хорошо поделится на 4 параллельных потока. И если пренебречь вычислением ε.
Только для спектра мне не хватит. При ширине 1024 я не вижу необходимые детали. Нужно 2048. А это 200+ ГБ памяти. Поэтому трехмерный случай — это сложно. Если не разрабатывать код с кеширующими ССД.
P.S. Оценки скорости были довольно приблизительные. Я проверял Матлаб только на малых задачах. Сейчас проверил Java — задачу 2048*1976 (аналог 2000*2000) на 4-ядернике. Время расчета 45,5 секунд. Ускорение от Матлаба 141 раз (точно).
Возможные планы на будущее:
*) Проверить скорость чистого С (не ++). По benchmarksgame он всегда быстрее.
1) Проверить комплексные классы в С и Java. Может, в С они реализованы достаточно быстро. Правда, боюсь, все они будут больше 8 байт.
2) Закинуть все 2- и 4-ядерные версии в MSVS, найти настройки оптимизации.
3) Проверить, могут ли лябмды/стримы ускорить основной цикл или дополнителные.
4) Сделать нормальный GUI для выбора всего и визуализации результатов.
99) Написать Cuda-версию.
Если кому-то интересно, опишу FDTD и другие методы рассчетов, фотонные кристаллы.
На Github выложил 2 версии:
1) 2-поточная с зачатками интерфейса выбора параметров
2) 4-поточная
Обе рисуют картинку и спектр. Просто пока пиксель в пиксель — не берите ширину выше 2048. Еще умеют принимать размеры области из консоли.
Автор: vlanko






