Написано в сотрудничестве с Р. Бухрадзе и К. Перминовым
1. Введение
Offline oбмен сообщениями сейчас является одним из наиболее популярных способов общения (1, 2, 3) — судя по аудитории способов общения и динамике её роста.
При этом, ключевым требованием при обмене сообщениями всегда будет являться полное соответствие отправленного сообщения – полученному, то есть передача данных не должна необратимо искажать сами данные. Естественное желание – сэкономить привело к созданию алгоритмов сжатия данных, которые, убирают естественную избыточность данных минимизируя объём хранимых и передаваемых файлов.
Максимально достигаемый объём сжатия, гарантирующий однозначное восстановление данных, определяется работами К. Шеннона по теории информации, и в общем-то является непреодолимым так как изъятие не только избыточной, но и смысловой информации не позволит однозначно восстановить исходное сообщение. Стоит отметить, что отказ от точного восстановления в некоторых случаях и не является критически важным и используется для эффективного сжатия графических, видео и музыкальных данных, где потеря несущественных элементов оправдана, однако о общем случае целостность данных, куда важнее их размера.
Соответственно интересным является вопрос о том, можно-ли не нарушая положения теории информации передать сообщение объёмом меньше, чем минимальный объём, который может быть достигнут при самом лучшем сжатии данных.
2. Пример
Поэтому давайте разберём пример, который позволит изучить особенности передачи информации. И хотя в «английской» традиции участников информационного обмена принято именовать Алиса и Боб, мы же в преддверии нового года воспользуемся более знакомыми любителями месседжинга: Матроскиным и Шариком соответственно.
В качестве же сообщения m выберем: «Поздравляю тебя, Шарик, ты балбес!». Длина его в односимвольной кодировке- len(m) — 34 байта.
Можно заметить, что длина сообщения заметно больше количества информации в нём. Это можно проверить вычеркивая из сообщения сначала каждый десятый символ, потом, (опять же из оригинального сообщения) каждый девятый и так далее до каждого четвёртого, результатом чего будет — «Позравяю ебя Шаик,ты албс!»-26 байт. Соответственно степень «загадочности» будет постепенно повышаться, но, догадаться о чём речь, будет достаточно просто. Более того, «Яндекс» распознаёт данное обращение.
Ещё более высокой степени сокращения длины сообщения при сохранении смысла можно добиться отбрасывая гласные и часть пробелов: “Пздрвл тб,Шрк,т блбс!” — 21 байт, стоит отметить, что хотя поисковики и не справляются таким написанием, восстановить фразу труда не составляет.
Если же посмотреть на количество информации I(m) в этом сообщении определяемое более строго через понятие информационной энтропии, то видно, что объём информации передаваемый в этом сообщении, составляет примерно 34*4,42/8=18,795 байт. Здесь: 4.42 бит/символ среднее количество информации в одном байте русского языка (4, 5), а 8 — приведение от битов к байтам. Это показывает, что воспользовавшись самым лучшим способом сжатия данных необходимо будет затратить не менее 19 байт на передачу сообщения от Матроскина Шарику.
Более того, верно и обратное утверждение о том, что передать нужное нам сообщение без потерь меньше чем за 19 байт невозможно (К. Шеннон, Работы по теории информации и кибернетике., изд. Иностранной литературы, Москва, 1963г.) Теорема 4. стр. 458.
3. Дальнейшие рассуждения
Однако продолжим… Пусть у Матроскина и у Шарика есть некоторое дополнительное количество информации k и пара функций, одна из которых m'=E(k,m), рассчитывающая пересечение дополнительной информации k и исходного сообщения m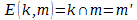 
, а вторая D(k,m') =m — обратная к E. Причём количество информации определяемой по Шеннону, удовлетворяет следующему условию: 
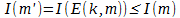. Соответственно, если нам удастся построить определённую выше пару функций E(k,m) и *D(k,m'), такие, что выполняются следующие два условия:
,
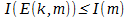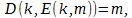
то это будет означать, что для передачи информации между адресатами может потребоваться меньше информации чем содержится в исходном сообщении.
При этом стоит обратить внимание на то, что по определению указанных функций не происходит нарушения утверждений теории информации.
Похожие, алгоритмы предусматривающие замену передаваемой информации её хешем, активно используются в системах оптимизации сетевого трафика. При этом, однако, в отличие от описываемого алгоритма, для того, чтобы эффективно использовать данный вид оптимизации требуется хотя бы однократная передача данных.
Ввиду того, что сообщения на естественном языке содержат объём данных, больший чем объём информации, то если предварительно сжать исходное сообщение при помощи какого-либо из алгоритмов, обеспечивающих эффективное устранение избыточности, например, арифметического кодирования.
Обозначим применение операции сжатия m’= Ar(m) такой, что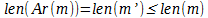 
. Если теперь использовать определённую выше функцию E над предварительно сжатым сообщением, то можно заметить, что и объём передаваемых данных и количество информации передаваемых между адресатами могут оказаться меньше объёма данных и количества информации в исходном сообщении.
То есть, обобщая: в предположении, что существует обратимое преобразование D(k,E(k,m)) =m, такое, что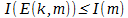 
применение операций устранения избыточности даёт возможность передать объём и количество информации в объёме не превосходящие соответствующие параметры (длина len(m) и количество информации I(m)) исходного сообщения.
В общем осталось только подобрать функции…..
Автор: Rumyantsev
