(продолжение. Предыдущая часть: «Автоматика из ДНК и белков: что у нее общего с электроникой?»)
Мы остановились на том, что лактозный оперон похож на логический элемент AND. Но откуда у него берутся цифровые свойства? Ведь оба входных сигнала (концентрации цАМФ и лактозы), вообще-то, аналоговые. Попробуем нарисовать входные функции лактозного оперона.
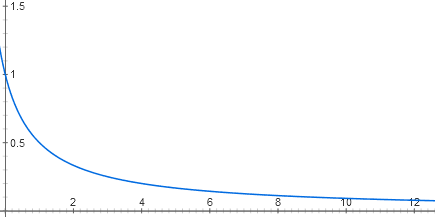
Каждый вход лактозного репрессора состоит из двух этапов молекулярного узнавания. Лактоза связывается с лактозным репрессором, а репрессор — с ДНК. В клетке находится несколько десятков молекул репрессора, каждая из которых, пока нет лактозы, может связываться с началом лактозного оперона. Когда она там связана, РНК-полимераза не может начать работу. Из-за теплового движения молекулы репрессора то и дело отваливаются от ДНК и присоединяются обратно. Если репрессора нет совсем, оперон работает на полную мощность (сейчас для простоты считаем, что катаболический активатор есть в избытке). При малых концентрациях репрессора он снижает активность оперона практически линейно. Но дальше эффект каждой новой порции репрессора все меньше и меньше, и в целом график зависимости близок к гиперболе y = 1 / (x + 1)
Например, у нас есть реакция, в которой из веществ А и В образуется вещество С. Реакция обратима, то есть С может распадаться обратно на А и В в тех же самых условиях:
A + B <-> C
В колбе, где идет эта реакция, установится какое-то равновесие между прямым и обратным направлением реакции. В системе будут все три вещества А, В и С в каких-то концентрациях (в физической химии концентрацию вещества принято обозначать его символом в квадратных скобках, [A], [B] и [C] в нашем примере). Закон действующих масс связывает равновесные концентрации веществ между собой: произведение концентраций продуктов, деленое на произведение концентраций исходных веществ, постоянно.
[C] / ([A] * [B]) = K
Буквой К здесь обозначена константа равновесия реакции. Она зависит только от химической природы реакции (т. е. какие вещества реагируют) и от температуры. Концентрации веществ, давление, катализаторы и прочие факторы не влияют на константу равновесия.
Например, если мы добавим в колбу побольше исходного вещества А, то равновесие сдвинется в сторону вещества С, его концентрация возрастет, а концентрация вещества В (которого мы не добавляли) при этом упадет. Однако отношение [C] к ([A] * [B]) останется постоянным.
Итак, у нас есть обратимая реакция связывания активной формы репрессора с опероном: RepA + OpA <-> Op (связывание репрессора превращает активную форму оперона в неактивную). Она имеет свою константу равновесия К{R-O} = [Op] / ([OpA] * [RepA]). Нам надо получить отсюда зависимость [ОрА] (количества активной формы оперона) от [RepA] (концентрации репрессора). Еще мы знаем, что в клетке только один лактозный оперон, который может быть в активной или неактивной форме: [Op] + [OpA] = 1
Из второго уравнения выражаем [Op] через [OpA] и подставляем в первое уравнение:
К{R-O} = (1 — [OpA]) / ([OpA] * [RepA])
После преобразований получаем:
[OpA] = 1 / (K{R-O} * [RepA] + 1)
То есть функция имеет вид y = 1 / (x + 1)
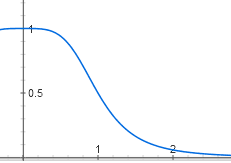
Молекулы репрессора плавают в клетке и связываются с ДНК только пачками по четыре. Чтобы активная форма репрессора превратилась в неактивную, она должна связаться с четырьмя молекулами лактозы — одной или двух недостаточно, надо по одной молекуле лактозы на каждую белковую субъединицу счетверенного репресора. Пока лактозы в клетке мало, ее молекулы связываются с репрессором по одной-две и он остается активным. Но после некоторой пороговой концентрации лактозы большинство молекул репрессора связывают по четыре молекулы лактозы и переходят в неактивную форму. График активности репрессора в зависимости от количества лактозы поэтому имеет S-образную форму и описывается функцией вида y = 1 / (1 + x^4).
RepA + 4 Lac <-> Rep
В уравнении для константы равновесия в этом случае появляются степени:
К{R-L} = [Rep] / ([RepA] * [Lac]^4)
Опять мы используем тот факт, что суммарная концентрация обоих форм репрессора постоянна: [Rep] + [RepA] = n, где n ≈ 50
И получаем, что [RepA] = n / (К{R-L} * [Lac]^4 + 1)
Теперь, чтобы получить входную характеристику оперона по лактозе, надо подставить вторую функцию в первую. Она будет с точностью до коэффициентов иметь такой вид:
y = 1 / (1 + (1 / (1 + x^4)))
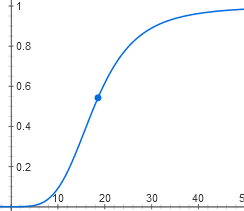
Ее график тоже S-образно изгибается. Получается, что лактозный оперон не реагирует на малые концентрации лактозы. При достижении пороговой концентрации появляются неактивные молекулы репрессора, связавшие по четыре лактозы, и оперон довольно резко включается.
Второй регуляторный вход лактозного оперона тоже состоит из двух шагов молекулярного узнавания: цАМФ связывается с активатором, а активатор — с ДНК. Отличие от лактозного входа в том, что здесь связывание молекул (активатора или цАМФ) повышает активность того, с чем они связались (оперона или активатора). То есть графики будут выходить из нуля и приближаться к горизонтальной прямой где-то выше оси Х.
2 цАМФ + Akt <-> AktA
Константа равновесия K{Ц-А} = [AktA] / ([Akt] * [цАМФ]^2)
Опять мы пользуемся тем, что сумма концентраций [AktA] и [Akt] постоянна, так как в клетке есть около 100 молекул активатора, переходящих между активной и неактивной формой. Выражая [Akt] через [AktA], получаем:
K{Ц-А} = [AktA] / ((100 — [AktA]) * [цАМФ]^2)
[AktA] = K{Ц-А} * [цАМФ]^2 / (1 + K{Ц-А} * [цАМФ]^2)
То есть зависимость [AktA] от [цАМФ] имеет вид y = x^2 / (1 + x^2)
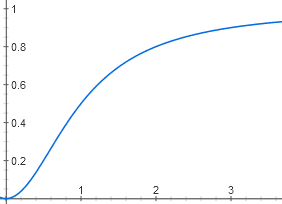
Из-за связывания двух молекул цАМФ график выглядит не как гипербола, а как S-образная кривая. Хотя пороговый эффект на ней заметен слабее, чем на графике для лактозы, потому что степень не четвертая, а только вторая.
Зависимость активности оперона от количества активатора имеет другой нюанс. Если связывание репрессора подавляет оперон почти полностью (где-то до 0,1%, что ниже погрешности биохимических измерений), то отсутствие активатора подавляет активность только до 5%. Поэтому график будет выходить не из нуля, а из точки (0; 0,05):
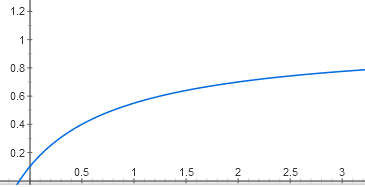
y = 0,05 + (0,95 * x / (1 + x))
Активность = [OpA] + 0,05 * [Op]
Зависимость [OpA] от [AktA] мы можем легко вывести по аналогии с предыдущими тремя. Активатор связывается по одной штуке, значит, [AktA] будет входить в формулу в первой степени. Он активирует оперон, значит, [AktA] будет и в числителе, и знаменателе:
[OpA] = K{А-O} * [AktA] / (K{А-O} * [AktA] + 1)
То есть функция имеет вид y = x / (1 + x)
И это только вклад оперона, связанного с активатором! Чтобы учесть вклад оперона без активатора, надо добавить слагаемое (1 — эта дробь) * 0,05. К счастью, оба слагаемых имеют общий знаменатель, поэтому функция усложняется совсем немного:
y = 0,05 + (0,95 * x / (1 + x))
Осталось получить зависимость активности оперона от концентрации цАМФ.
Для этого надо подставить первую формулу (для концентрации активного CAP в зависимости от концентрации цАМФ) во вторую формулу (для активности оперона от концентрации активного САР)…
… И получить четырехэтажную дробь:
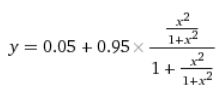
У нас получилась самая сложная функция из всех в этой статье. Впрочем, ее график выглядит похоже на график более простой зависимости активного CAP от концентрации цАМФ, y = x^2 / (1 + x^2):
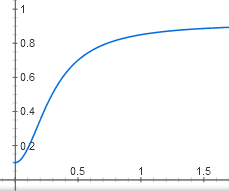
Тоже S-образная кривая с некоторым пороговым эффектом, которая медленно приближается к горизонтали y = 1. Только начинается не из нуля, а из точки (0; 0,05).
Осталось понять, как взаимодействуют два входа. В случае лактозного оперона ответ простой — никак. Лактозный репрессор и катаболический активатор не влияют на связывание друг друга с ДНК. Поэтому связывание этих двух белков можно считать независимыми событиями. Полная активность оперона достигается, когда и активатор связан, и репрессор не связан. Вероятность такого совпадения равна произведению вероятностей каждого из них по отдельности. Значит, чтобы получить функцию активности лактозного оперона от двух переменных ([Lac]) и ([цАМФ]), надо просто перемножить функции от каждой этой переменной:
Активность = (1 / (1 + (1 / (1 + [Lac]^4)))) * (0,05 + 0,095 * ([цАМФ]^2 / (1 + [цАМФ]^2)) / (1 + ([цАМФ]^2 / (1 + [цАМФ]^2))))
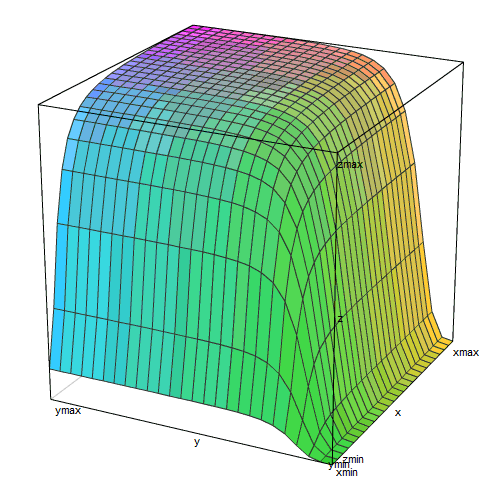
Трехмерный график этой функции
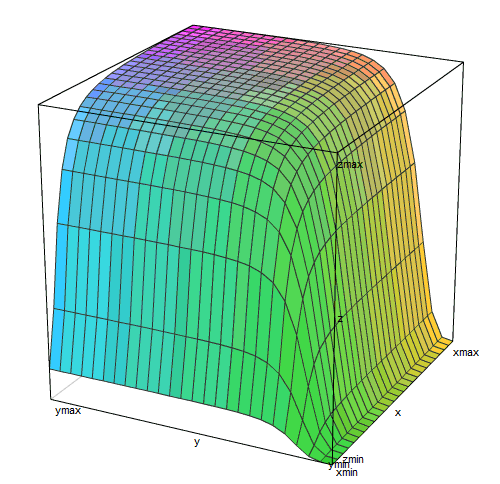
похож на плато, обрывающееся ущельями по двум сторонам. Правое ущелье (малые концентрации лактозы) более глубокое и плоскодонное, чем левое (малые концентрации цАМФ).
В реальной жизни кишечной палочки вокруг нее лактозы либо нет совсем (чаще всего), либо ее концентрация выше пороговой и лактозный репрессор практически не мешает работе оперона (когда хозяин съел что-то молочное). Концентрация цАМФ — это внутренний сигнал, который вырабатывается самой клеткой. Она тоже бывает либо слишком малой для включения лактозного оперона (когда есть глюкоза или крахмал), либо достаточной для включения на 95% и более (если ничего вкуснее лактозы нет). То есть почти всегда лактозный оперон находится в условиях либо плато на этом графике, либо в одном из ущелий.
Входные функции лактозного оперона измерены экспериментально. Способ измерения напоминает прием отладки микроконтроллеров «повесить светодиод на выходную ногу». Берется регуляторная область оперона и соединяется с геном зеленого флуоресцентного белка. Эта генная конструкция вставляется в клетки кишечной палочки, из которой удаляется штатный лактозный оперон (чтобы концентрация лактозы была жестко задана экспериментатором) и штатная система, кодирующая голод уровнями цАМФ. После этого активность лактозного оперона можно точно измерять спектрофотометром по уровню зеленой флюоресценции. Оказывается, что в пределах точности измерений (1%) теория полностью сходится с экспериментом (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC164651/)
Дно левого ущелья на графике входной функции (при малых концентрациях цАМФ) находится выше нуля. Это не баг, а фича: благодаря ей при наличии нескольких сахаров сразу, кишечная палочка оказывается готова быстро переключиться на лактозу, когда глюкоза кончится. Мутанты кишечной палочки, у которых регуляторная функция лактозного оперона ближе к чистому AND (то есть без цАМФ оперон не работает), переключаются с глюкозы на лактозу по часу и более: в момент исчерпания глюкозы у них нет ферментов усвоения лактозы, а значит, нет и энергии, чтобы их быстро сделать. Нормальная кишечная палочка («дикий тип») встречает этот момент, уже имея сколько-то ферментов усвоения лактозы и ей хватает 15-20 минут для полного переключения на новый сахар.
Теперь отвлечемся от лактозного оперона и посмотрим шире, на что способны логические элементы на такой химической базе. Практически везде в биохимических сигнальных системах мы встречаем молекулярное узнавание, которое описывается функциями вида y = x^n / (1 + x^n) для активаторов и y = 1 / (1 + x^n) для репрессоров. Степень n в этих функциях показывает количество связываемых однотипных молекул для получения эффекта, и бывает обычно равна 1, 2 или 4 (чаще всего 2). Можно получить более сложные логические ключи, добавляя в начало оперона больше сайтов связывания регуляторных белков. Этих белков может быть больше двух типов. Эффекты разных белков на посадку РНК-полимеразы могут складываться (OR) или перемножаться (AND). Но в целом мы будем иметь дело с какой-то комбинацией (сложением или перемножением) базовых функций y = x^n / (1 + x^n) и y = 1 / (1 + x^n) с разными степенями и коэффициентами.
Некоторые интересные функции получаются очень просто. Например, один и тот же регуляторный белок может связываться (в спаренной форме) с двумя участками промотора. В одном участке он действует как репрессор, а в другом — как активатор. Для работы оперона надо, чтобы сайт репрессора был пуст, а сайт активатора — занят. Получается функция с четким максимумом:
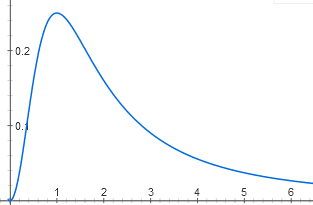
y = (1/ (1 + x^2)) * (x^2 / (1 + x^2))
Без этого белка оперон неактивен, потому что пуст сайт активатора, а при высоких концентрациях он неактивен, потому что занят сайт репрессора. Максимальная активность будет, когда и сайт активатора, и сайт репрессора заняты с вероятностью 50%.
Еще можно сделать два сайта связывания активатора, в одном активатор будет сильно связываться с ДНК, но слабо активировать ген, в другом — слабо прикрепляться к ДНК, но сильно активировать ген. В этом случае получается функция вроде y = x^4 / (1 + x^4) + 0.3 * (10x)^4 / (1 + (10x)^4), со ступенчатым графиком:
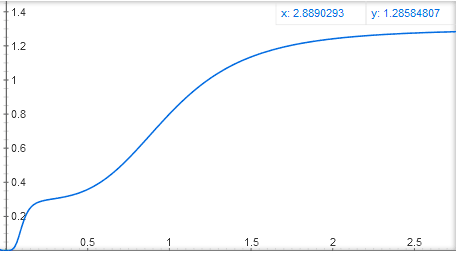
Математики, ау! Можете рассказать в комментариях, что еще можно и что нельзя получить при сложении и перемножении этих базовых функций y = x^n / (1 + x^n) и y = 1 / (1 + x^n)?
В следующей части займемся схемами из таких логических элементов.
Автор: HellMaus


