Фильмы, где огромные армии сходятся друг с другом на поле боя в эпичной битве обычно вызывают в людях бурю эмоций. Сцены сражений из "Звездных войн" с мастерски владеющими световыми мечами джедаями и ордами боевых дроидов — не исключение.
Но иногда бывает интересно посмотреть на сам процесс битвы как бы с высоты птичьего полета и увидеть весь ход развития событий. Для этого можно использовать различные средства виртуальной симуляции. В этом посте приведен пример моделирования битвы между боевыми дроидами Федерации и орденом Джедаев с помощью такой простой дискретной модели как клеточный автомат.

Клеточные автоматы
Представьте, что весь мир — это сетка, разбитая на квадраты, называемые клетками. Каждая из таких клеток может находиться в различных состояниях из заданного множества. На состояние клетки влияют состояния соседних клеток, которые обычно определяются через окрестность Мура порядка 1. Яркий пример такой модели — игра "Жизнь", придуманная математиком Джоном Конвеем в 1970-х. Ее правила предельно просты:
- Каждая клетка может быть либо "живой", либо "мертвой".
- Мертвая клетка, рядом с которой находится ровно 3 живые, на следующем ходу становится живой.
- Если рядом с живой клеткой находится 2 или 3 живые клетки, то на следующем ходу она продолжает жить.
- Если рядом с живой клеткой находится меньше 2 или больше 3 живых клеток, то она умирает.

Именно благодаря простоте описания правил подобных моделей мы и будем использовать клеточный автомат для моделирования эпичной битвы.
Придумываем свой автомат
Всего в нашем клеточном автомате будет 4 типа клеток — поле (зеленый), дроид (бежевый), джедай (голубой), бластер (красный). Теперь придумаем правила. Нам нужно, чтобы дроны сбивались в кучки и пускали лучи бластеров в джедаев, а джедаи, в свою очередь, атаковали эти густые кучки дроидов. Для простоты моделирования добавим клеткам новую возможность — перемещаться. По сути, перемещение клетки в клеточном автомате можно задать как переход одной из клеток в состояние переходящей, а саму переходящую перевести в нулевое состояние (в нашем случае это поле).
Что потребуется реализовать для создания симулятора битвы:
- Дроиды сбиваются в группы
- Дроид стреляет в ближайшего джедая в радиусе поражения
- Джедай атакует ближайший к нему отряд
Нахождение групп дроидов
Если представить дроидов как вершины графа, а соседних дроидов как связанные вершины, то группы дроидов — это компоненты связности такого графа. Их мы легко сможем получить по завершении каждого шага с помощью поиска в глубину (DFS):
components = []
var colors = new Array(field.grid.length)
colors.fill(0) // 0 is white, 1 is gray, 2 is black
for (var i = 0; i < field.grid.length; i++)
if (field.grid[i].color == 1)
if (colors[i] == 0) {
var center = dfs(colors, i)
components.push({ x: Math.round(center.x / center.k), y: Math.round(center.y / center.k) })
droidsAmount += center.k
}
Сама функция определения компоненты связности рекурсивна:
function dfs(colors, v) {
colors[v] = 1
var x = field.grid[v].x, y = field.grid[v].y, k = 1
for (var i = 0; i < field.grid[v].n.length; i++)
if (field.grid[field.grid[v].n[i]].color == 1 && colors[field.grid[v].n[i]] == 0) {
var newPos = dfs(colors, field.grid[v].n[i])
x += newPos.x
y += newPos.y
k += newPos.k
}
colors[v] = 2
return { x: x, y: y, k: k }
}Свойство k соответствует числу дроидов в группе и требуется для вычисления центра группы (среднего арифметического по x- и y-координатам каждого дроида). Каждый дроид обращается к своим соседям, координаты которых передаются в первый вызов рекурсии, который, в свою очередь, вернет суммы всех координат дроидов, а также их количество.
Движение к цели
У всех участников сражения есть цели — клетки, на которые они стремятся попасть: джедай — в центр ближайшей группы дроидов, дроиды — к своим союзникам, а снаряд — в клетку с координатами, где находился джедай в тот момент, когда был сделан выстрел.
function moveToTarget(n, me, priority, ban) {
var newX = me.x, newY = me.y
var deltaX = me.tx - me.sx, deltaY = me.ty - me.sy
var scope = deltaY / deltaX
if ((deltaX == 0) || (deltaY == 0)) {
newX = me.x + (deltaX == 0 ? 0 : deltaX / Math.abs(deltaX))
newY = me.y + (deltaY == 0 ? 0 : deltaY / Math.abs(deltaY))
} else {
if (Math.abs(scope) >= 1) {
newY = me.y + deltaY / Math.abs(deltaY)
newX = me.sx + Math.round((newY - me.sy) / (scope))
} else {
newX = me.x + deltaX / Math.abs(deltaX)
newY = me.sy + Math.round((newX - me.sx) * (scope))
}
}
if (!set(n, { x: newX, y: newY }).length) {
me.color = 0
return false
}
var newCell = set(n, { x: newX, y: newY })[0]
for (var key in ban)
if (newCell[key] == ban[key])
return false
return { x: newX, y: newY, instead: { color: 0 }, priority: priority }
}Рассмотрим, как это работает. Расстояние между целью и начальным положением объекта по оси X обозначим за deltaX, по оси Y — за deltaY. Понятно, что если изначальная x-координата объекта имеет большее значение, чем координата цели, то deltaX будет отрицательно. То же самое касается deltaY.
Обозначим отношение deltaY к deltaX как scope(наклон). Если наклон больше единицы, то на каждом шагу объект сдвигается на единицу по оси Y, и иногда — по оси X. Тогда newY = me.y + deltaY / Math.abs(deltaY), где деление на абсолютное значение позволяет получить единицу с правильным знаком. Так как движение можно определить как
x = y / scope, то newX = me.sx + Math.round((newY — me.sy) / (scope)). Аналогично поступаем для случаев с scope < 1.
Бывают случаи, когда объект и цель находятся в одинаковом столбце или одинаковой строке. Тогда может возникнуть деление на ноль. Для таких случаев делается проверка (deltaX == 0) || (deltaY == 0). Если это правда, то мы просто проверяем с помощью тернарного оператора разность координат, и, если ее значение ненулевое, прибавляем единицу с правильным знаком.
В параметре ban прописаны свойства, которые недопустимы для клетки, на которую объект переходит. Например, дроид не должен наталкиваться на других роботов. Следовательно, для дроида ban = { color: 1 } (1 — индекс цвета дроида). Если клетка, на которую объект хочет перейти, будет обладать хотя бы одним свойством, имеющим равное значение с одноименным свойством ban, перемещения не будет.
Если объект попытается попасть на несуществующую клетку (переместиться за границу поля), то он исчезает с карты.
Но если все прошло успешно, то в качестве новых координат функция вернет newX и newY.
Алгоритм дроида
Дроид делает выстрелы в сторону ближайшего джедая. Радиус видимости дроида задается коэффициентом k2. Дроид выбирает ближайшего джедая, выстрел в которого не задел бы дроидов, находящихся в радиусе длины 5.
Коэффициент k2 — дистанция обнаружения джедая дроидом.
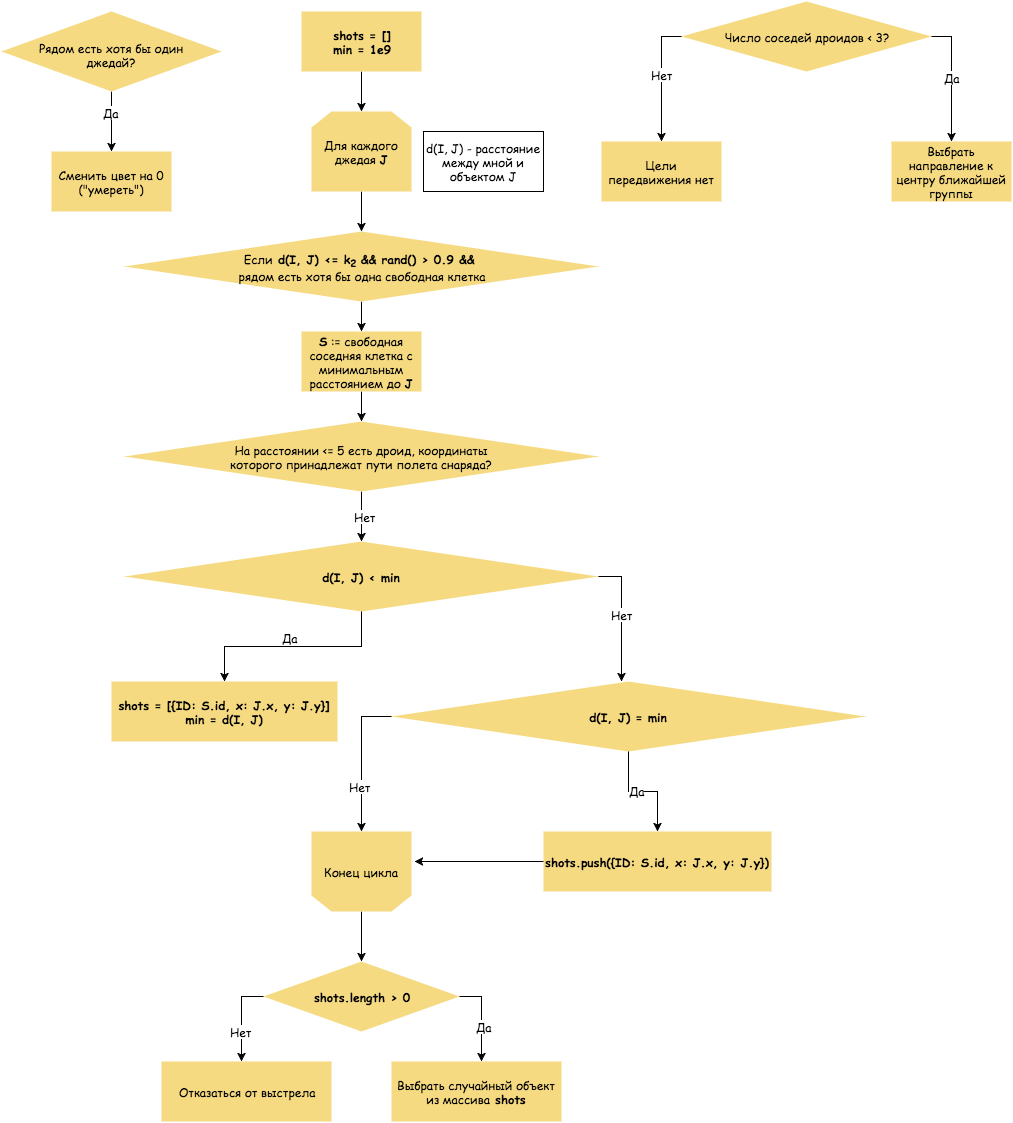
Алгоритм джедая
Для вычисления оптимального направления удара джедая зададим в соответствие каждой окружающей его клетке вес, который будем вычислять следующим образом:
Джедая окружает 8 клеток (в случае, если джедай находится в углу или у границы поля — 3 или 5 клеток). Вес вычисляется отдельно для каждой из этих клеток и зависит от состояний остальных клеток вокруг джедая. Представим вес как полином вида 5a1 + 4b1 + 4b2 + 3c1 + 3c2 + 2d1 + 2d2 + 1e, где каждая переменная равняется единице если соответствующая клетка занята дроидом, в противном случае она равна нулю. Чем дальше клетка находится от обрабатываемой, тем меньше коэффициент при соответствующем ей одночлене.
Пример вычисления веса клетки можно увидеть на рисунке:

Веса клеток при конкретной ситуации:
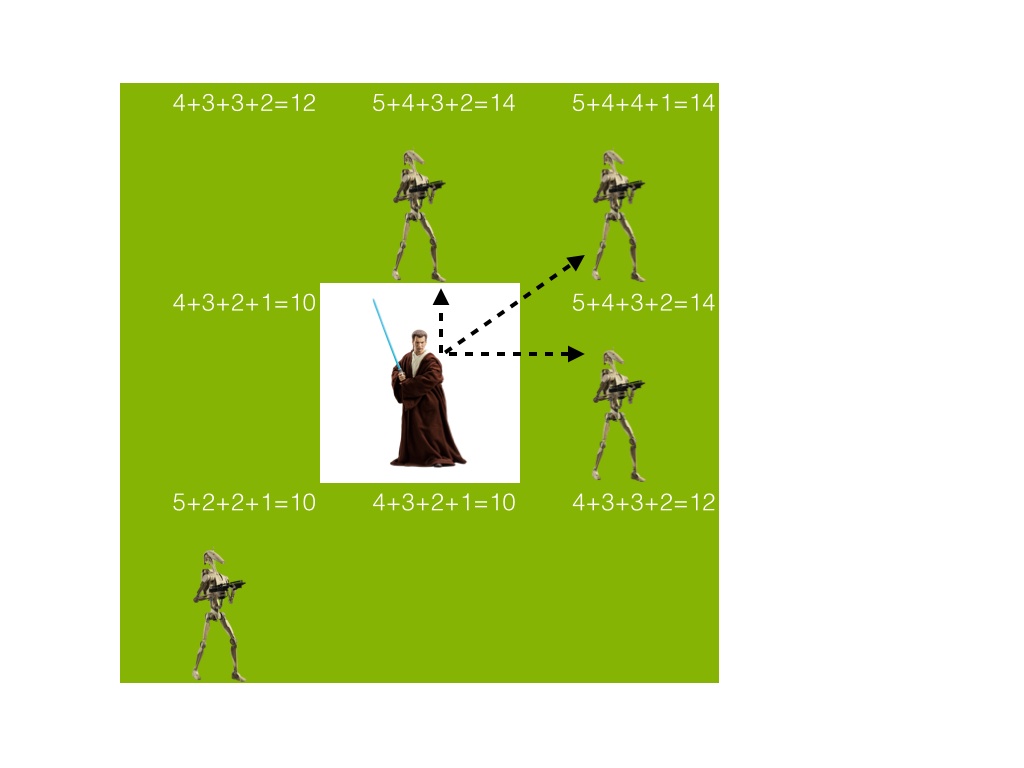
В приведенном случае джедай имеет три оптимальных варианта передвижения. Один из них будет выбран случайным образом.
Осталось помочь джедаю обнаружить скопления дроидов. Если представить дроидов как вершины графа, которые связаны в случае соседства дроидов, то после каждого шага с помощью поиска в глубину(DFS) мы сможем найти все компоненты связности этого графа, записать координаты их центров и количество дроидов в компоненте в массив. На следующем шаге джедаи ищут ближайшие к себе отряды и немедленно устремляются к ним.
Коэффициент k1 — максимально число снарядов, от которых джедай может увернуться. По умолчанию k1 = 4.
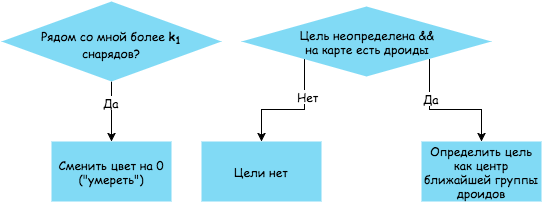
Полет снаряда
Бесконечно снаряд лететь не может, так что после 32 шагов он исчезает:
function processBullet(n, me) {
me.age++
if (me.age > 32)
me.color = 0
}Движение его предельно просто — обычный вызов функции направления к цели:
function moveBullet(n, me) {
return moveToTarget(n, me, 1, {})
}Неприятные фишки
Что уж говорить — программа, формально выполняя строго заданный алгоритм, иногда может удивлять нас странными результатами.
Наиболее заметным является "эффект мертвых джедаев". Джедаи стоят мертво и кучно.


Почему? Ответ прост: один из джедаев достиг цели и пытается выбраться из толпы, но остальные джедаи мешают ему это сделать. Они, в свою очередь, пытаются протиснуться к цели, но так как она занята и находящийся там джедай не может ее покинуть, возникает данная ситуация.
Моделируем сражение
Поиграться с симуляцией можно прямо в браузере. Выберите тип клеток и начните рисовать им по экрану, пока не получите желаемое расположение. Нажмите на "Start" и наслаждайтесь битвой. Если битва закончилась или просто наскучила вам, можно начать на "Stop", после чего сгенерируются графики. На первом будет показано количество дроидов в определенные моменты времени, на втором — такая же статистика для джедаев.
» Поиграться с симуляцией можно на тут
Для создания графиков использовалась библиотека Chart.js. О чем могут говорить графики?
- Количество дроидов до определенного момента оставалось одинаковым. На том шаге, когда число дроидов начало снижаться, произошло первое столкновение джедаев с дроидами.
- Самые частые случаи гибели джедаев. Был ли боец поражен снарядом до того, как вклинился в ряды противника, или же пал в самый разгар битвы, окруженный численно превосходящим противником? Все это можно узнать, сравнив на двух графиках момент его смерти.
- Общая картина боя. Шел ли он плавно, или были «передышки» и «кульминационные моменты»? Посмотрим, есть ли резкие скачки в графе и получим ответ на вопрос!
Заключение
Исходный код с комментариями доступен на GitHub. Для запуска скачайте репозиторий и откройте index.html в своем браузере.
Получилось, на мой взгляд, занятное зрелище. Графики позволяют собирать информацию о ходе боев при различных начальных конфигурациях. Интересно, как бы выглядели графики настоящих исторических сражений? Разумеется, в этом посте рассматривается вымышленная вселенная, но настоящие исторические битвы проходили примерно по тем же правилам: солдаты сбивались в группы, атаковали друг друга и, разумеется, несли потери.
Впрочем, одной симуляцией ограничиваться не стоит — ведь есть еще более интересная задача, а именно нахождение наилучшего алгоритма действий для каждого участника сражения. И тут исследователю поможет теория игр. Но это уже совсем другая история...
Автор: Volvox


