В первой части я забыл упомянуть, что если случайно сгенерированные данные не по душе, то можно взять любой подходящий пример отсюда. Можно почувствовать себя ботаником, виноделом, продавцом. И все это не вставая со стула. В наличии множество наборов данных и одно условие — при публикации указывать откуда взял данные, чтобы другие смогли воспроизвести результаты.
Градиентный спуск
В прошлой части был показан пример вычисления параметров линейной регрессии с помощью метода наименьших квадратов. Параметры были найдены аналитически — 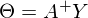 , где
, где 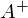 — псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).
— псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).
Проблема заключается в том, что вычисление псевдообратной матрицы очень затратно: 2 умножения по 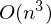 , нахождение обратной матрицы —
, нахождение обратной матрицы — 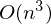 , умножение матрицы вектор
, умножение матрицы вектор 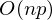 , где n — количество элементов в матрице A (количество признаков * количество элементов в тестовой выборке) Если количество элементов в матрице A велико (> 10^6 — например), то даже если в наличии 10000 ядер, нахождение решения аналитически может затянуться. Также первая производная может оказаться нелинейной, что усложнит решение, аналитического решения может не оказаться вовсе или данные могут просто не влезть в память и потребуется итеративный алгоритм. Бывает, что в плюсы записывают и то, что численное решение не идеально точное. В связи с этим функцию стоимости минимизируют численными методами. Задачу нахождения экстремума называют задачей оптимизации. В этой части я остановлюсь на методе оптимизации, который называется градиентный спуск.
, где n — количество элементов в матрице A (количество признаков * количество элементов в тестовой выборке) Если количество элементов в матрице A велико (> 10^6 — например), то даже если в наличии 10000 ядер, нахождение решения аналитически может затянуться. Также первая производная может оказаться нелинейной, что усложнит решение, аналитического решения может не оказаться вовсе или данные могут просто не влезть в память и потребуется итеративный алгоритм. Бывает, что в плюсы записывают и то, что численное решение не идеально точное. В связи с этим функцию стоимости минимизируют численными методами. Задачу нахождения экстремума называют задачей оптимизации. В этой части я остановлюсь на методе оптимизации, который называется градиентный спуск.
Не будем отходить от линейной регрессии и МНК и обозначим функцию потерь 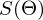 как
как 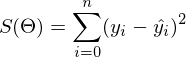 — она осталась неизменной. Напомню, что градиент — это вектор вида
— она осталась неизменной. Напомню, что градиент — это вектор вида 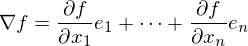 , где
, где 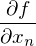 — это частная производная. Одним из свойств градиента является то, что он указывает направление, в котором некоторая функция f возрастает больше всего. Доказательство этого следует из определения производной. Пара доказательств. Возьмем некоторую точку a — в окрестности этой точки функция F должна быть определена и дифференцируема, тогда вектор антиградиента будет указывать на направление, в котором функция F убывает быстрее всего. Отсюда делается вывод, что в некоторой точке b, равной
— это частная производная. Одним из свойств градиента является то, что он указывает направление, в котором некоторая функция f возрастает больше всего. Доказательство этого следует из определения производной. Пара доказательств. Возьмем некоторую точку a — в окрестности этой точки функция F должна быть определена и дифференцируема, тогда вектор антиградиента будет указывать на направление, в котором функция F убывает быстрее всего. Отсюда делается вывод, что в некоторой точке b, равной 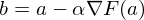 , при некотором малом
, при некотором малом 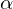 значение функции будет меньше либо равным значению в точке а. Можно представить это, как движение вниз по холму — сделав шаг вниз, текущая позиция будет ниже, чем предыдущая. Таким образом, на каждом следующем шаге высота будет как минимум не увеличиваться. Формальное определение. Исходя из этих определений можно получить формулу для нахождения неизвестных параметров (это просто переписанная версия формулы выше):
значение функции будет меньше либо равным значению в точке а. Можно представить это, как движение вниз по холму — сделав шаг вниз, текущая позиция будет ниже, чем предыдущая. Таким образом, на каждом следующем шаге высота будет как минимум не увеличиваться. Формальное определение. Исходя из этих определений можно получить формулу для нахождения неизвестных параметров (это просто переписанная версия формулы выше):
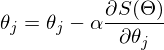
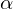 — это шаг метода. В задачах машинного обучения его называют скоростью обучения.
— это шаг метода. В задачах машинного обучения его называют скоростью обучения.
Метод очень прост и интуитивен, возьмем простой двумерный пример для демонстрации:
Необходимо минимизировать функцию вида 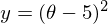 . Минимизировать значит найти при каком значении
. Минимизировать значит найти при каком значении 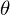 функция
функция 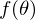 принимает минимальное значение. Определим последовательность действий:
принимает минимальное значение. Определим последовательность действий:
1) Необходима производная по 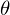 :
: 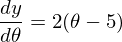
2) Установим начальное значение 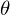 = 0
= 0
3) Установим размер шага — попробуем несколько значений — 0.1, 0.9, 1.2, чтобы посмотреть как этот выбор повлияет на сходимость.
4) 25 раз подряд выполним указанную выше формулу: 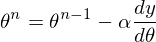 Так как неизвестный параметр только один, то и формула только одна.
Так как неизвестный параметр только один, то и формула только одна.
Код крайне прост. Исключая определение функций, весь алгоритм уместился в 3 строки:
STEP_COUNT = 25
STEP_SIZE = 0.1 # Скорость обучения
def func(x):
return (x - 5) ** 2
def func_derivative(x):
return 2 * (x - 5)
previous_x, current_x = 0, 0
for i in range(STEP_COUNT):
current_x = previous_x - STEP_SIZE * func_derivative(previous_x)
previous_x = current_x
print("After", STEP_COUNT, "steps theta=", format(current_x, ".6f"), "function value=", format(func(current_x), ".6f"))
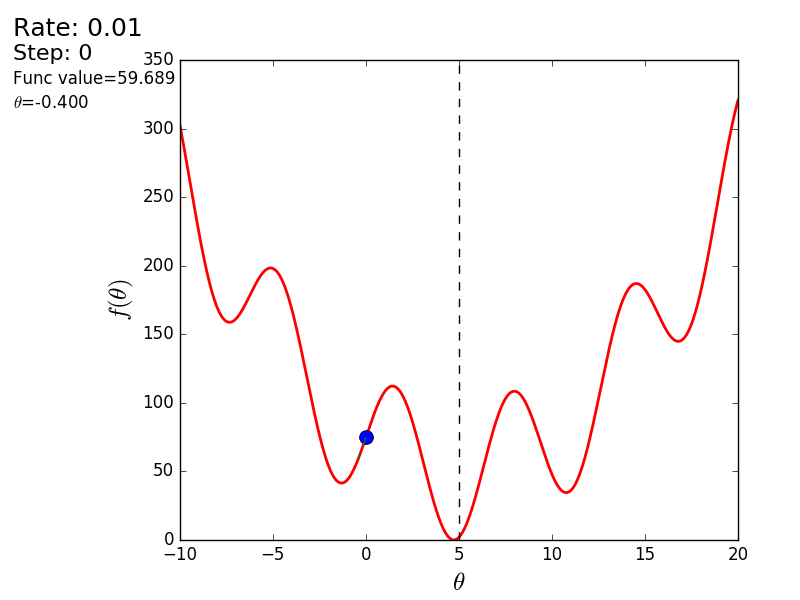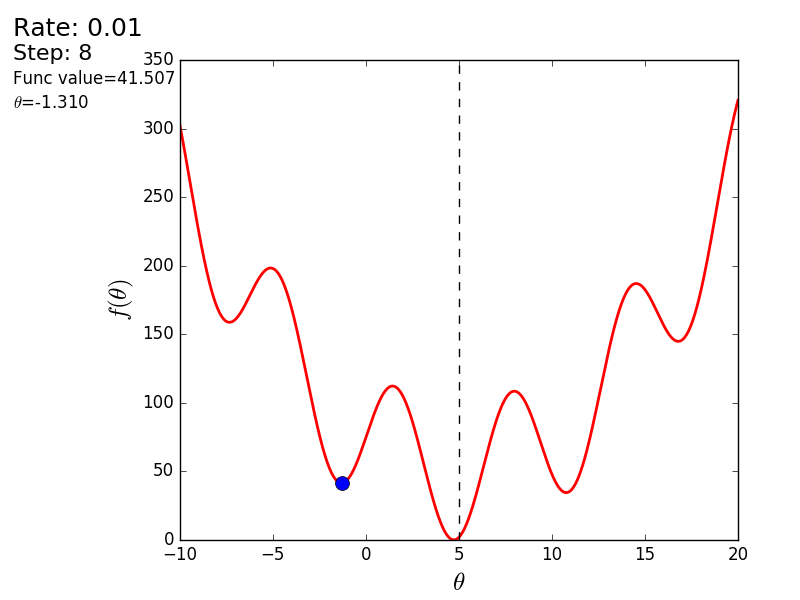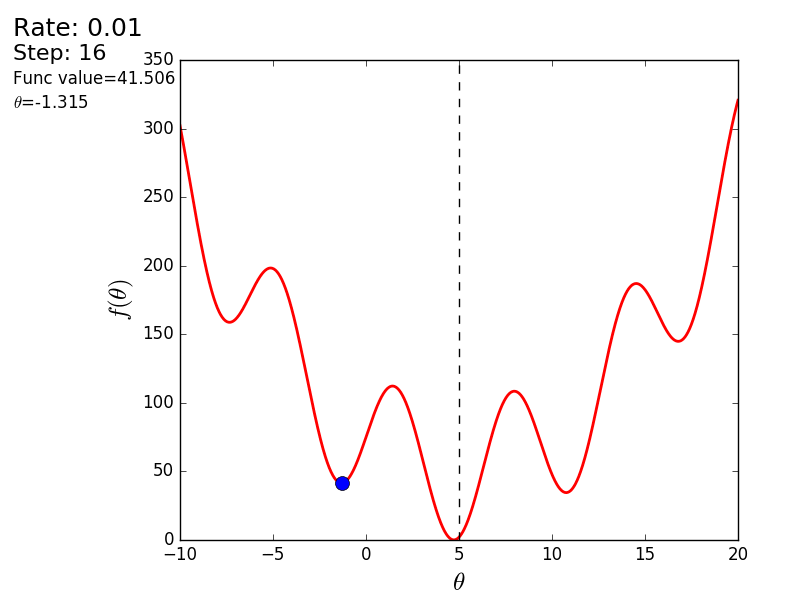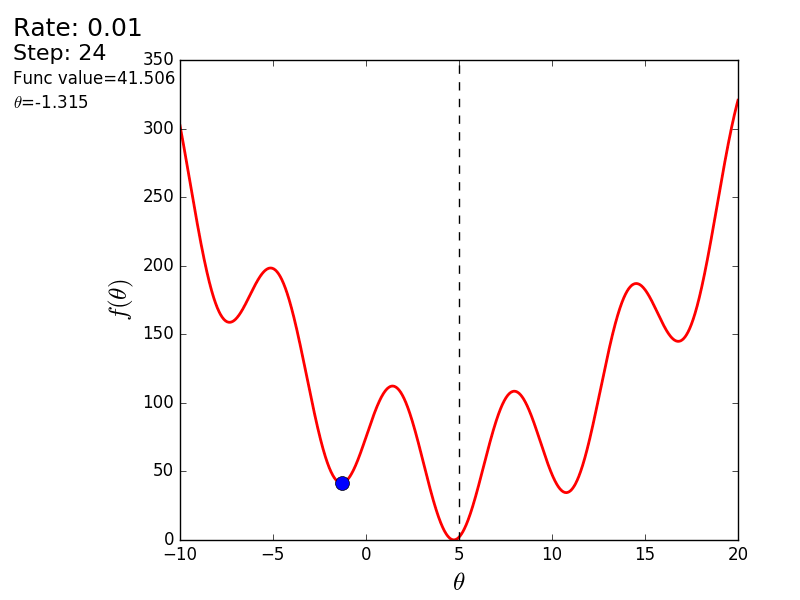
Весь процесс можно визуализировать примерно так (синяя точка — значение на предыдущем шаге, красная — текущее):
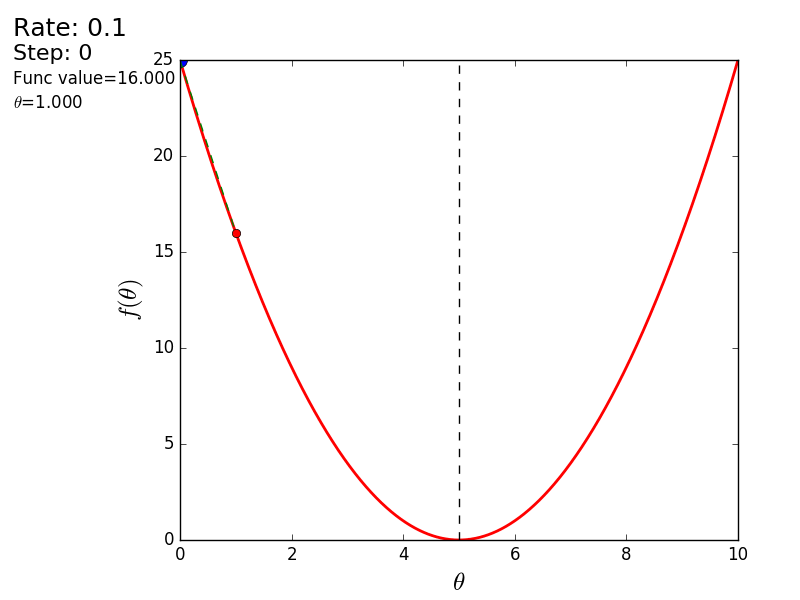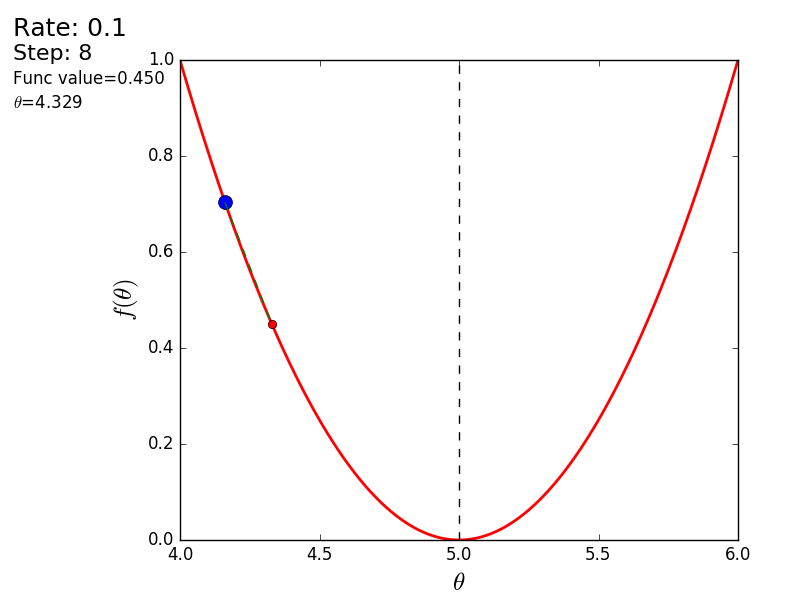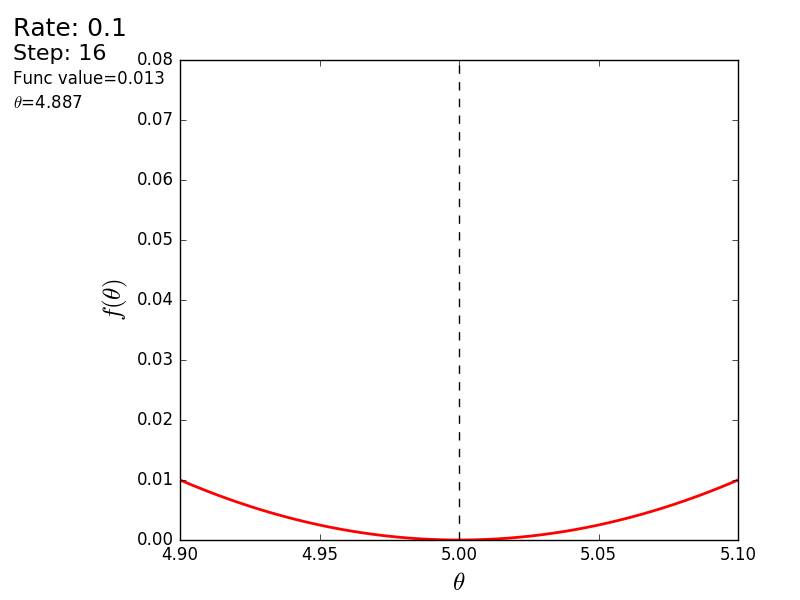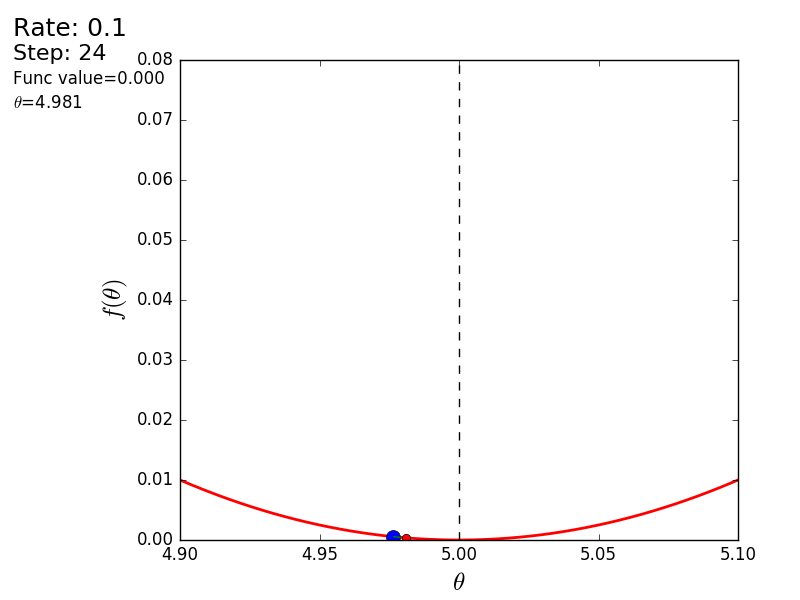
Или же для шага другого размера:
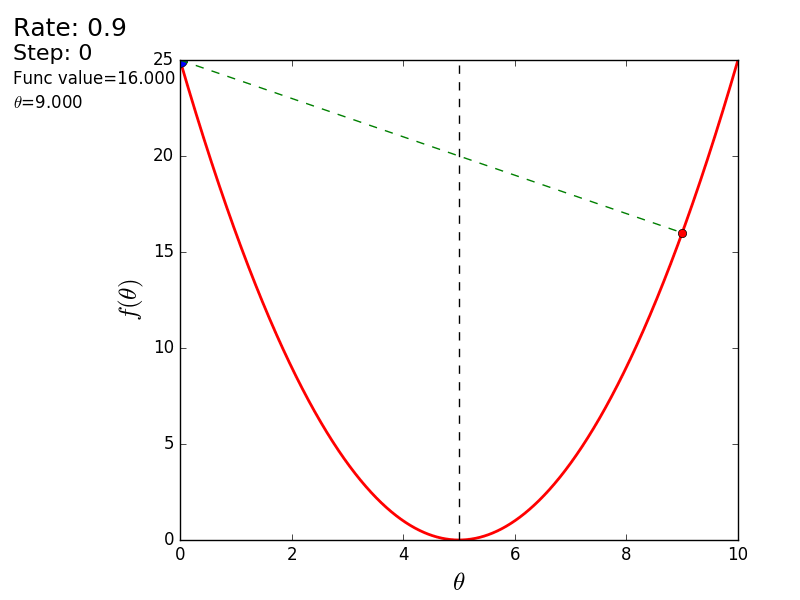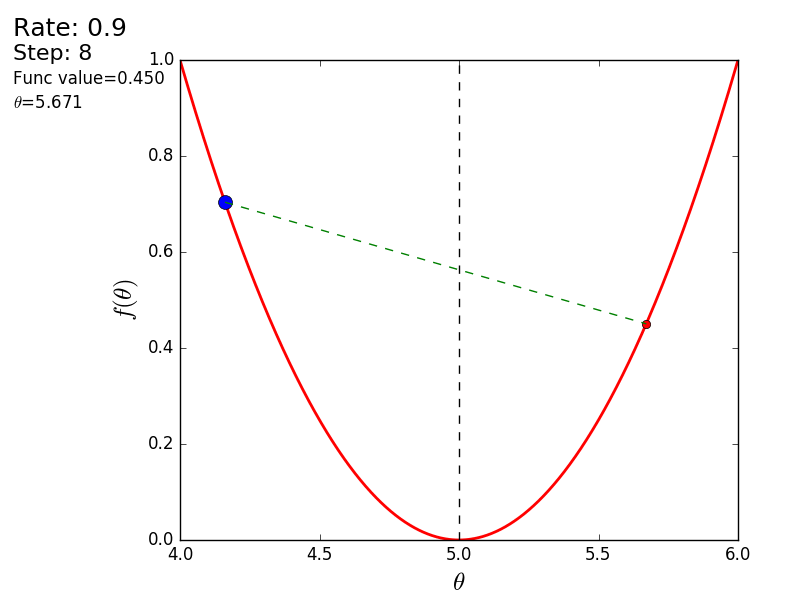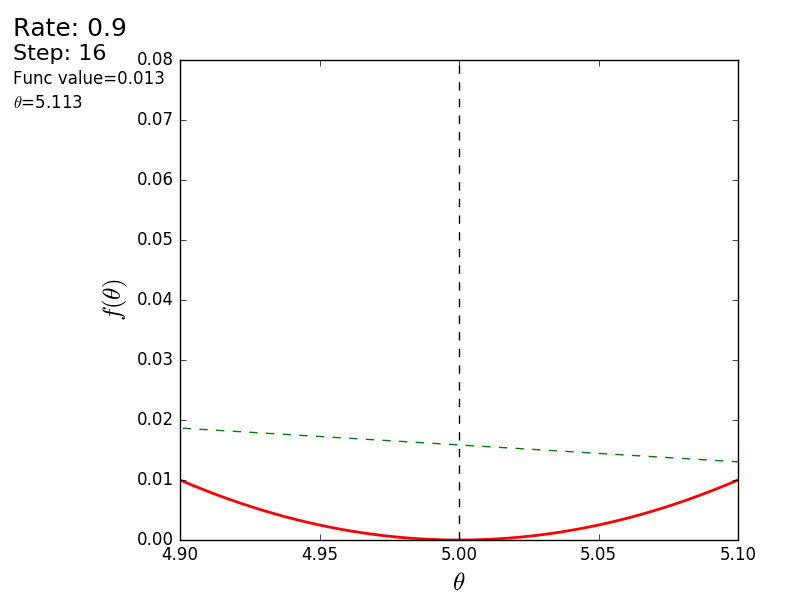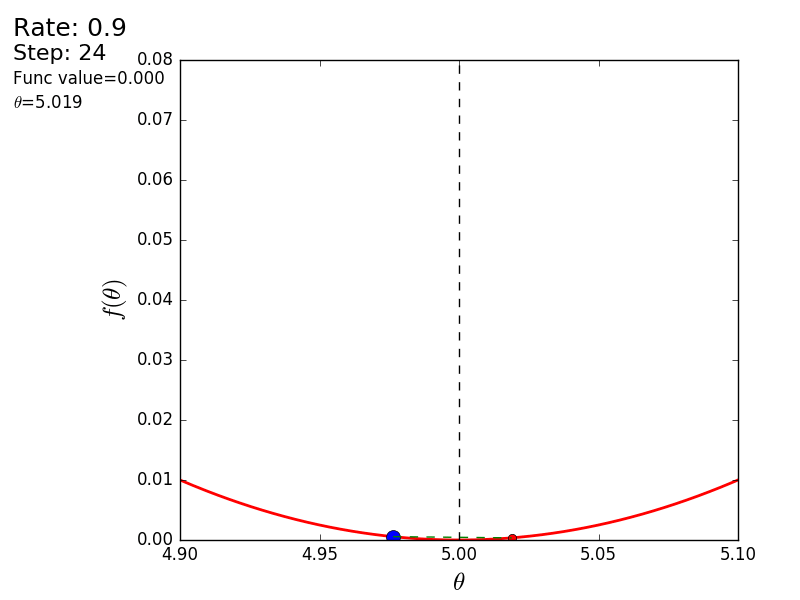
При значении, равном 1.2, метод расходится, каждый шаг опускаясь не ниже, а наоборот выше, устремляясь в бесконечность. Шаг в простой реализации подбирается вручную и его размер зависит от данных — на каких-нибудь ненормализованных значениях с большим градиентом и 0.0001 может приводить к расхождению.
import matplotlib.pyplot as plt
import matplotlib.animation as anim
import numpy as np
STEP_COUNT = 25
STEP_SIZE = 0.1 # Скорость обучения
X = [i for i in np.linspace(0, 10, 10000)]
def func(x):
return (x - 5) ** 2
def bad_func(x):
return (x - 5) ** 2 + 50 * np.sin(x) + 50
Y = [func(x) for x in X]
def func_derivative(x):
return 2 * (x - 5)
def bad_func_derivative(x):
return 2 * (x + 25 * np.cos(x) - 5)
# Какая-то жажа и первый кадр пропускается
skip_first = True
def draw_gradient_points(num, points, line, cost_caption, step_caption, theta_caption):
global previous_x, skip_first, ax
if skip_first:
skip_first = False
return points, line
current_x = previous_x - STEP_SIZE * func_derivative(previous_x)
step_caption.set_text("Step: " + str(num))
cost_caption.set_text("Func value=" + format(func(current_x), ".3f"))
theta_caption.set_text("$\theta$=" + format(current_x, ".3f"))
print("Step:", num, "Previous:", previous_x, "Current", current_x)
points[0].set_data(previous_x, func(previous_x))
points[1].set_data(current_x, func(current_x))
# points.set_data([previous_x, current_x], [func(previous_x), func(current_x)])
line.set_data([previous_x, current_x], [func(previous_x), func(current_x)])
if np.abs(func(previous_x) - func(current_x)) < 0.5:
ax.axis([4, 6, 0, 1])
if np.abs(func(previous_x) - func(current_x)) < 0.1:
ax.axis([4.5, 5.5, 0, 0.5])
if np.abs(func(previous_x) - func(current_x)) < 0.01:
ax.axis([4.9, 5.1, 0, 0.08])
previous_x = current_x
return points, line
previous_x = 0
fig, ax = plt.subplots()
p = ax.get_position()
ax.set_position([p.x0 + 0.1, p.y0, p.width * 0.9, p.height])
ax.set_xlabel("$\theta$", fontsize=18)
ax.set_ylabel("$f(\theta)$", fontsize=18)
ax.plot(X, Y, '-r', linewidth=2.0)
ax.axvline(5, color='black', linestyle='--')
start_point, = ax.plot([], 'bo', markersize=10.0)
end_point, = ax.plot([], 'ro')
rate_capt = ax.text(-0.3, 1.05, "Rate: " + str(STEP_SIZE), fontsize=18, transform=ax.transAxes)
step_caption = ax.text(-0.3, 1, "Step: ", fontsize=16, transform=ax.transAxes)
cost_caption = ax.text(-0.3, 0.95, "Func value: ", fontsize=12, transform=ax.transAxes)
theta_caption = ax.text(-0.3, 0.9, "$\theta$=", fontsize=12, transform=ax.transAxes)
points = (start_point, end_point)
line, = ax.plot([], 'g--')
gradient_anim = anim.FuncAnimation(fig, draw_gradient_points, frames=STEP_COUNT,
fargs=(points, line, cost_caption, step_caption, theta_caption),
interval=1500)
# Для того, чтобы получить гифку необходимо установить ImageMagick
# Можно получить .mp4 файл без всяких magick-shmagick
gradient_anim.save("images/animation.gif", writer="imagemagick")
Вот еще пример с «плохой» функцией. В первой анимации метод также расходится и будет долго блуждать по холмам из-за слишком высокого шага. Во втором случае был найден локальный минимум и варьируя значение скорости не получится заставить метод найти минимум глобальный. Этот факт является одним недостатков метода — он может найти глобальный минимум только если функция выпуклая и гладкая. Или если повезет с начальными значениями.
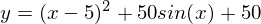
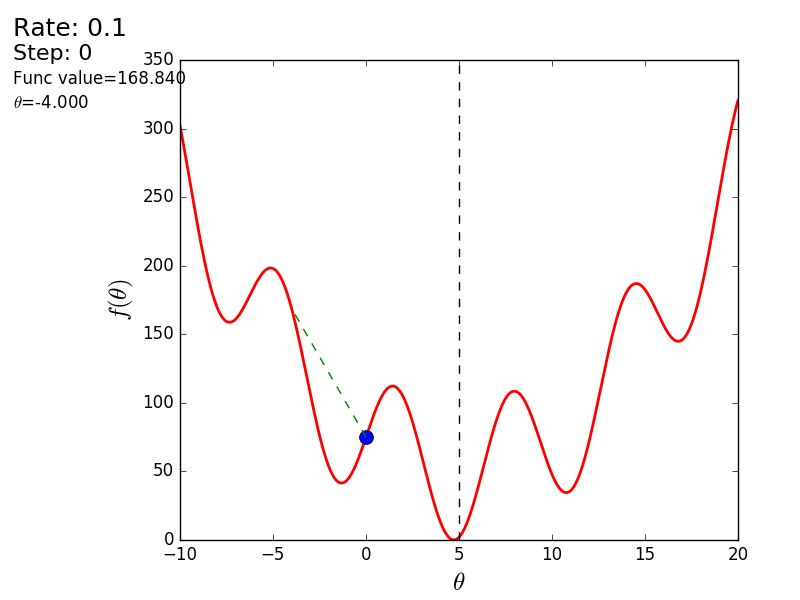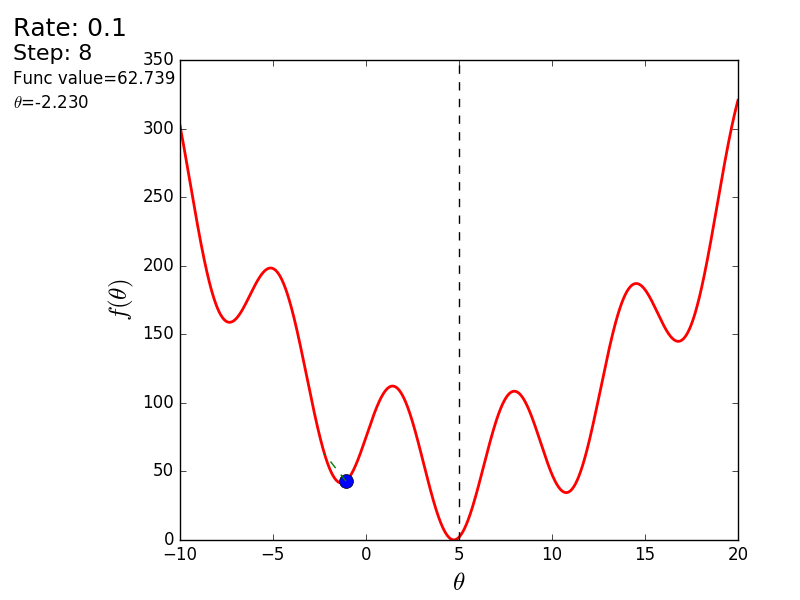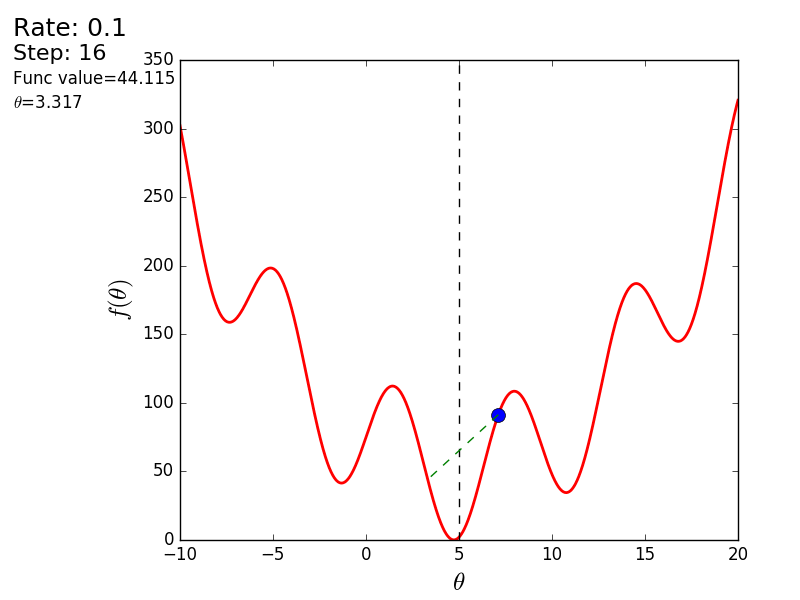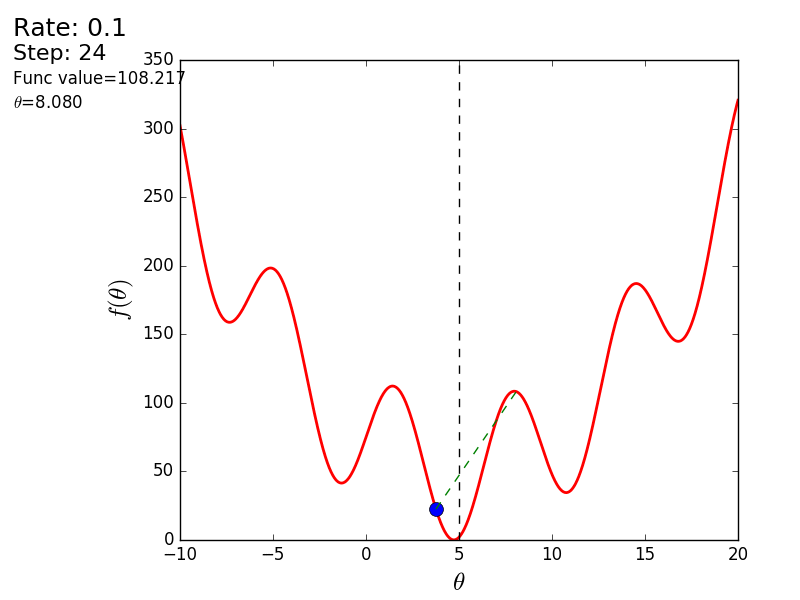
Также возможно рассмотреть работу алгоритма на трехмерном графике. Часто рисуют только изолинии какой-то фигуры. Я взял простой параболоид вращения: 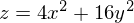 . В 3D выглядит он так:
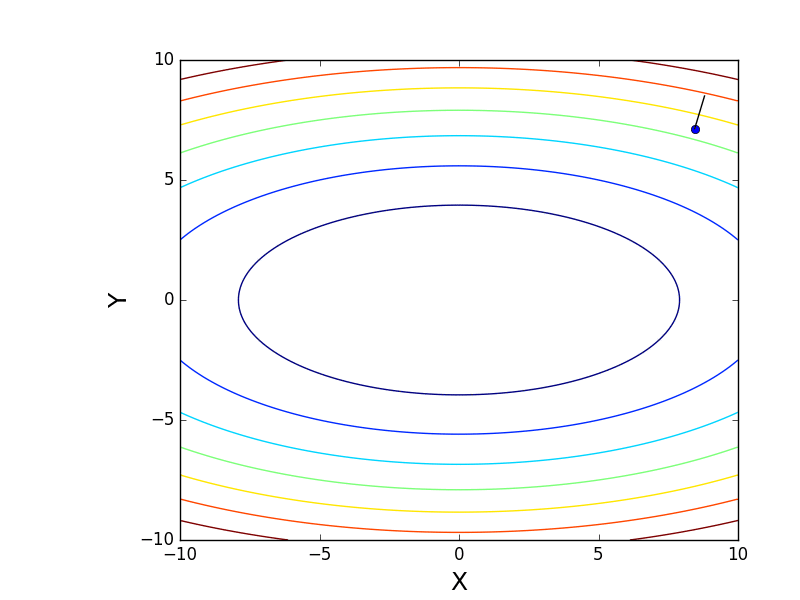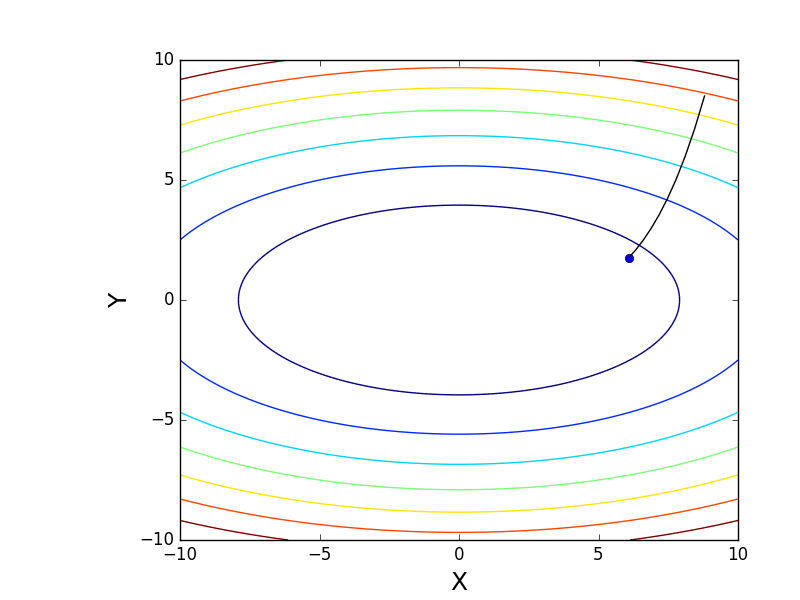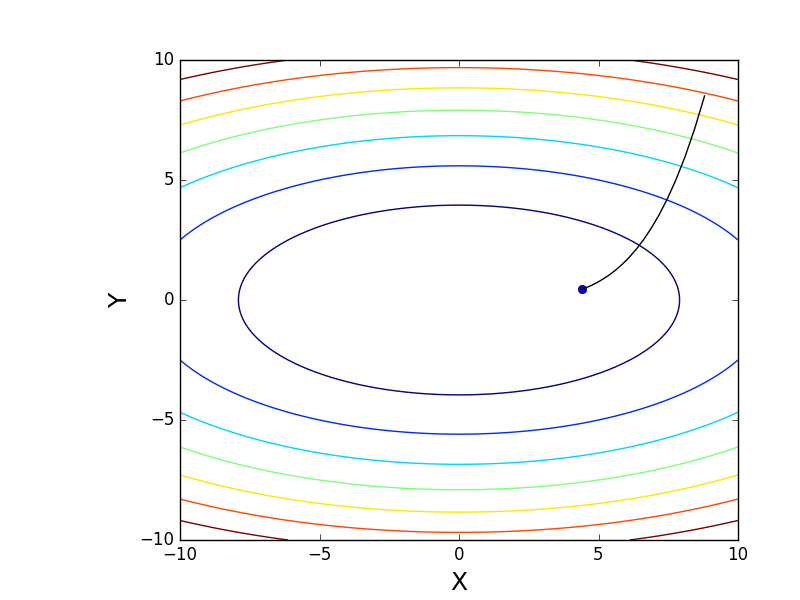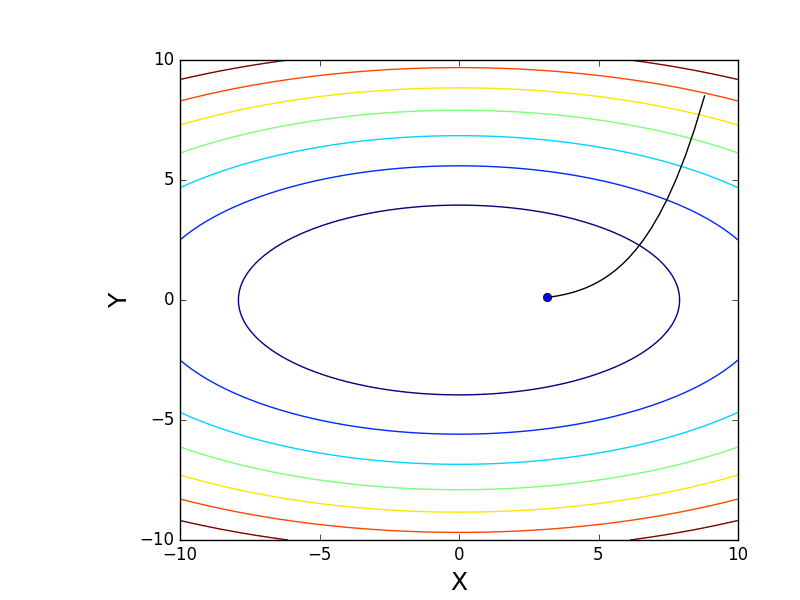
. В 3D выглядит он так: 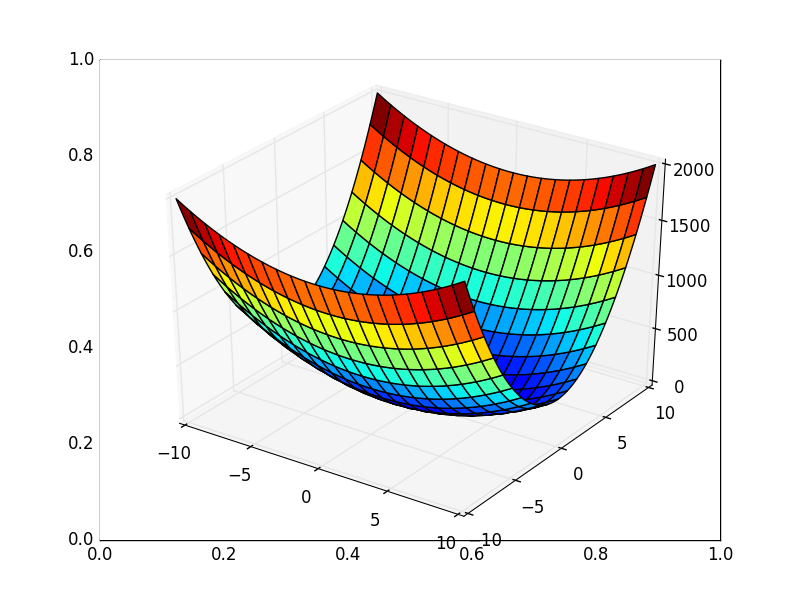 , а график с изолиниями — «вид сверху».
, а график с изолиниями — «вид сверху».
import matplotlib.pyplot as plt
import matplotlib.animation as anim
import numpy as np
STEP_COUNT = 25
STEP_SIZE = 0.005 # Скорость обучения
X = np.array([i for i in np.linspace(-10, 10, 1000)])
Y = np.array([i for i in np.linspace(-10, 10, 1000)])
def func(X, Y):
return 4 * (X ** 2) + 16 * (Y ** 2)
def dx(x):
return 8 * x
def dy(y):
return 32 * y
# Какая-то жажа и первый кадр пропускается
skip_first = True
def draw_gradient_points(num, point, line):
global previous_x, previous_y, skip_first, ax
if skip_first:
skip_first = False
return point
current_x = previous_x - STEP_SIZE * dx(previous_x)
current_y = previous_y - STEP_SIZE * dy(previous_y)
print("Step:", num, "CurX:", current_x, "CurY", current_y, "Fun:", func(current_x, current_y))
point.set_data([current_x], [current_y])
# Blah-blah
new_x = list(line.get_xdata()) + [previous_x, current_x]
new_y = list(line.get_ydata()) + [previous_y, current_y]
line.set_xdata(new_x)
line.set_ydata(new_y)
previous_x = current_x
previous_y = current_y
return point
previous_x, previous_y = 8.8, 8.5
fig, ax = plt.subplots()
p = ax.get_position()
ax.set_position([p.x0 + 0.1, p.y0, p.width * 0.9, p.height])
ax.set_xlabel("X", fontsize=18)
ax.set_ylabel("Y", fontsize=18)
X, Y = np.meshgrid(X, Y)
plt.contour(X, Y, func(X, Y))
point, = plt.plot([8.8], [8.5], 'bo')
line, = plt.plot([], color='black')
gradient_anim = anim.FuncAnimation(fig, draw_gradient_points, frames=STEP_COUNT,
fargs=(point, line),
interval=1500)
# Для того, чтобы получить гифку необходимо установить ImageMagick
# Можно получить .mp4 файл без всяких magick-shmagick
gradient_anim.save("images/contour_plot.gif", writer="imagemagick")
Также обратите внимание, что все линии градиента, направлены перпендикулярно изолиниям. Это означает, что двигаясь в сторону антиградиента, не получится за один шаг сразу же прыгнуть в минимум — градиент указывает совсем не туда.
После графического пояснения, найдем формулу для вычисления неизвестных параметров 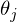 линейной регрессии с МНК.
линейной регрессии с МНК.
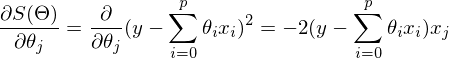
Если бы количество элементов в тестовой выборке было равно единице, то формулу можно было бы так и оставить и считать. В случае, когда в наличии n элементов алгоритм выглядит так:
Повторять v раз
{
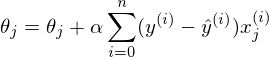
для каждого j одновременно.
}, где n — количество элементов в обучающей выборке, v — количество итераций
Требование одновременности означает, что производная должна быть вычислена со старыми значениями theta, не стоит вычислять сначала отдельно первый параметр, затем второй и т.д., потому что после изменения первого параметра отдельно, производная также изменит свое значение. Псевдокод одновременного изменения:
for i in train_samples:
new_theta[1] = old_theta[1] + a * derivative(old_theta)
new_theta[2] = old_theta[2] + a * derivative(old_theta)
old_theta = new_theta
Если вычислять значения параметров по одиночке, то это уже будет не градиентный спуск. Допустим, у нас трехмерная фигура и если вычислять параметры один за одним, то можно представить этот процесс как движение только по одной координате за раз — один шажок по x координате, затем шажок по y координате и т.д. ступеньками, вместо движения в сторону вектора антиградиента.
Приведенный выше вариант алгоритма называют пакетный градиентный спуск. Количество повторений можно заменить на фразу «Повторять, пока не сойдется». Эта фраза означает, что параметры будут корректироваться до тех пор, пока предыдущее и текущее значения функции стоимости не сравняются. Это значит, что локальный или глобальный минимум найден и дальше алгоритм не пойдет. На практике равенства достичь невозможно и вводится предел сходимости  . Его устанавливают какой-нибудь малой величиной и критерием остановки является то, что разность предыдущего и текущего значений меньше предела сходимости — это значит, что минимум достигнут с нужной, установленной точностью. Выше точности (меньше
. Его устанавливают какой-нибудь малой величиной и критерием остановки является то, что разность предыдущего и текущего значений меньше предела сходимости — это значит, что минимум достигнут с нужной, установленной точностью. Выше точности (меньше  ) — больше итераций алгоритма. Выглядит это как-то так:
) — больше итераций алгоритма. Выглядит это как-то так:
while abs(S_current - S_previous) >= Epsilon:
# do something
Так как пост неожиданно растянулся, я бы хотел его на этом завершить — в следующей части я продолжу разбор градиентного спуска для линейной регрессии с МНК.
Для запуска примеров необходимы: numpy, matplotlib.
Для запуска примеров, создающих анимации необходим ImageMagick.
Материалы, использованные в статье — github.com/m9psy/neural_network_habr_guide
Автор: m9_psy





