Полиномиальный алгоритм для комбинаторной задачи (P=NP?)

В этой статье я хотел бы рассказать о моем исследовании на тему равенства классов P и NP. Оригинал статьи вы можете прочитать здесь.

Небольшое введение.

Вообще проблема равенства классов — одна из самых главных открытых математических проблем. Ведь при положительном ответе, программисты смогут гораздо оптимизировать многие аспекты программы, а так же деятели науки смогут например расшифровывать геном за короткое время. Однако, многие ученые склоняются к отрицательному ответу. Мне же, как программисту, не мыслим отрицательный ответ, да и если посмотреть, мы уже придумали алгоритмы, сокращающие время перебора во много раз, чем путем полного перебора.

В моей статье написано все достаточно замудрено и сложно для понимания, здесь я бы хотел рассказать по-простому об этом исследовании, а так же дополнить статью новыми интересными открытиями, а так же поделиться с вами этим полиномиальным алгоритмом, для быстрого вычисления комбинаторных задач такого рода.

Постановка задачи:

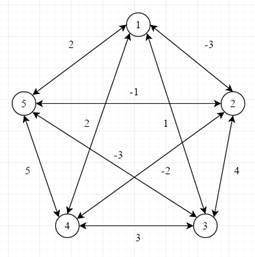
Это полный неориентированный граф. Полный — потому что все вершины взаимодействуют с другими, неориентированный — потому что у графа нет направлений.

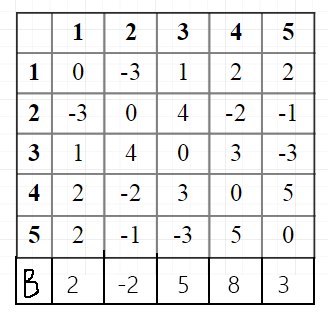
И удобнее графы рассматривать в виде разных матриц, к примеру мы будем рассматривать матрицу ребер, соединяющих вершины:

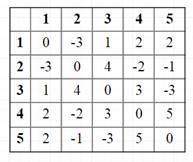
Можем представить эти 5 вершин как 5 сотрудников. Представим, что у нас есть для них поручение и мы знаем как сотрудники взаимодействуют друг с другом. К примеру 1 и 2 сотрудники справятся с этой задачей хуже (их комбинация -3), чем 1 и 4 (их комбинация 2). А допустим 1,3 и 4 сотрудники (их комбинация 1+2+3=6) выполняют задачу уже лучше. Главное понять как устроено нахождение комбинации. Если все еще сложно понять, то вот видео youtu.be/7rKXqprYR2E?t=1h8m52s. Постановка задачи такая же.

Задача сводится к тому, чтобы найти максимальное число в комбинациях.

Теперь решение.
Вообще обнаружить данное решение мне помогла формула: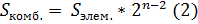
Sэлементов — найденное число в самой большой комбинации, в данном случае 12345. Либо сумма всех элементов матрицы, только поделенная на 2. Так как матрица симметричная относительно диагонали, делить мы можем.

Сейчас поговорим про разложение матрицы нахождение выгодных векторов, а так де оптимального вектора и уже решения, конечно в статье довольно сложно все описано, однако мы можем сделать это довольно быстро, приступим:

Для начала мы должны найти максимальный элемент в матрице — это 5 и комбинация ему соответствующая — 4,5.
Следующим шагом проверяем на наличие отрицательных элементов в матрице B, это можно сделать следующим образом:

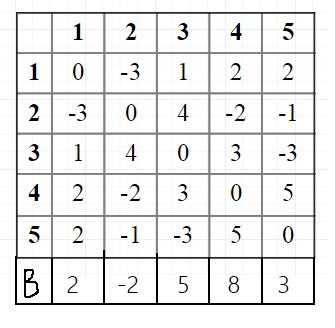
Мы складываем по вертикали (по горизонтали, не принципиально) все элементы и смотрим, есть ли здесь отрицательные числа, если нет, то комбинация будет максимальной, то есть 1,2,3,4,5. Однако здесь присутствует -2, идем дальше.

Следующий шаг — нахождение выгодных векторов. Через кучу транспонирований матрицы делать не удобно, тем более для программиста можно поступить следующим образом (однако дальше я покажу еще более выгодный способ):

Зачеркиваем строку, соответствующую выгодному вектору, а остальные элементы суммируем:

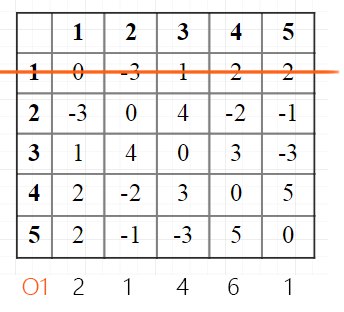
Выгодный вектор O1

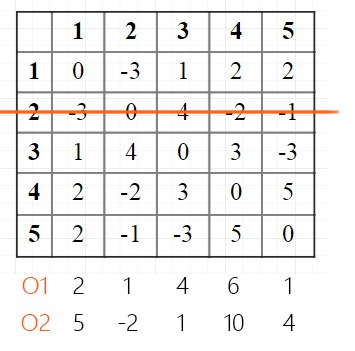
Выгодный вектор O2

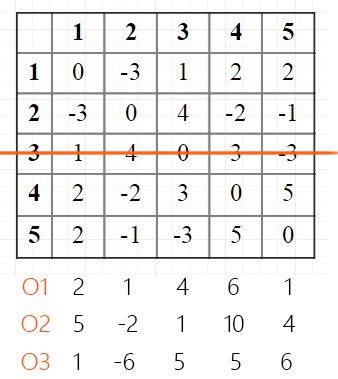
Выгодный вектор O3
И так далее до О5, и следом сразу же посчитаем сумму элементов в каждом векторе:

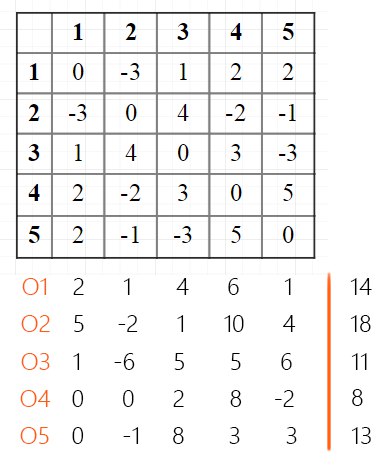
Находим самое большое число из сумм — 18, значит вектор O2 будет оптимальным и в нем содержится решение.
Рассмотрим алгоритм, как достать это решение. Находим в этом векторе отрицательные элементы и суммируем их, в нашем случае просто -2. Если мы домножим на минус единицу, поменяем знак, то получится разница. Разница между числом для самой большой комбинации и ответом, который нам нужно найти, если просто, то это x+r=y. x — либо сумма всех элементов деленная на 2, либо просто число от самой большой комбинации. Подставим в формулу, получим 8+2=10. Это будет числовое решение матрицы. Однако нам нужно узнать именно вершины (рабочие) составляющие комбинацию. Просто берем номера столбцов для всех положительных чисел вектора O2: 1,3,4,5. Эта комбинация и является искомой.

Зачем мы искали максимальный элемент (5) — если вдруг решение будет меньше, чем этот элемент, то комбинация будет соответствовать этому элементу, а не комбинации в векторе O.

Есть способ быстрее определить искомую комбинацию, без векторов O, однако мне важно, чтобы вы обратили внимание на полученную матрицу векторов O, если все ее элементы сложить, то получим сумму всех комбинаций (в данном случае 64, можете проверить по формуле выше). Тем самым, матрица является матрицей всех комбинаций графа (рабочих). То, как, например для графа размером 20х20, количество комбинаций — 1048575 и все они умещаются в эту матрицу 20 порядка, да еще и находится оптимальное решение, просто поражает!

А теперь немного шустрее решим эту задачу:

1. Выпишем сумму всех элементов и максимальное число.
2. Тут нам пригодится вектор B, от суммы всех элементов отнимаем каждый элемент и самый наибольший ответ определит выгодный вектор.

По примеру с O2: 16-(-2)=18. Мы намного сократили время выполнения алгоритма.
3. Дальше таким же способом как и ранее получаем вектор O2 и находим решение.

Количество шагов не превышает полинома второй степени, сами можете убедиться.

Немного скриншотов из программы по проверке:

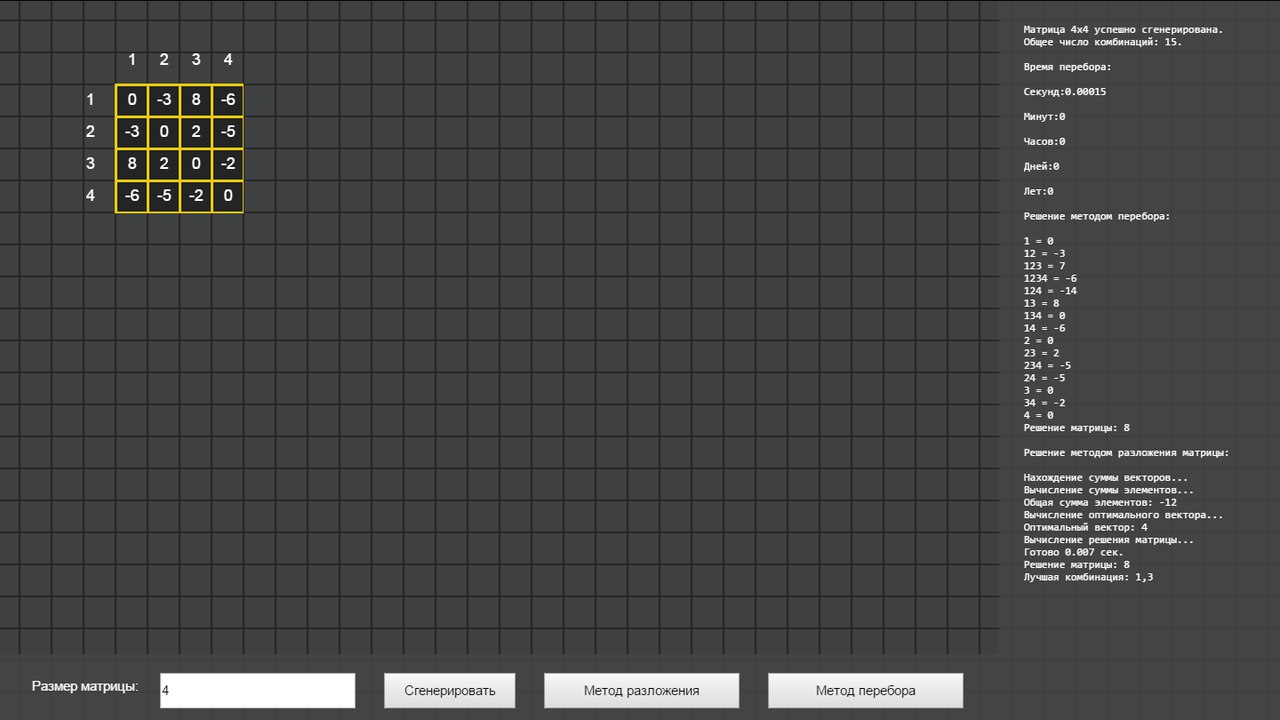
Матрица 4х4, метод разложения и перебора

Матрица 50х50, 0,039 сек. на решение

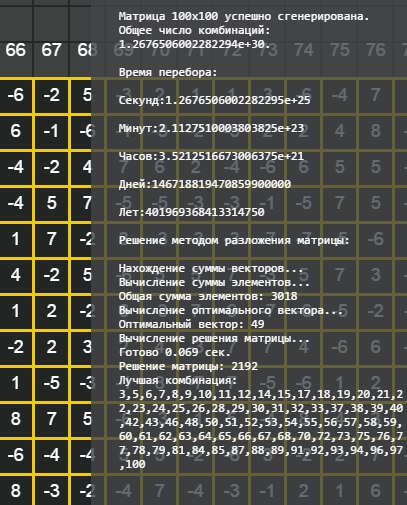
Матрица 100х100, 0,069 сек. на решение

Как же дела обстоят с другими задачами? С задачей коммивояжера дела обстоят хорошо, однако и не очень. Например если получить матрицу векторов O и матрицу векторов O для транспонированной матрицы, то мы опять же получим матрицу всех комбинаций, однако тут уже комбинаций гамильтоновых циклов:

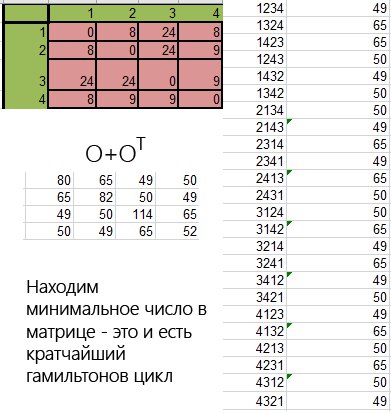
На самом деле я еще не до конца разобрался с задачей коммивояжера, однако для графа n=4 это работает, а для графов n>4, не работает, потому что нужно немного перестраивать матрицы комбинаций, пока я еще не понял каким образом.

Этот алгоритм на самом деле может помочь в многих задачах по планированию, как, например, та же задача по отбору сотрудников для задачи по эффективности, идеальные программы тренировок, питания, в принципе применение неограниченное.

Матрица комбинаций — вещь не до конца известная мне и я был бы рад, если бы вы помогли понять, что это такое и как с этим работать.

Автор: Eponesh

Источник