В этой статье я расскажу, как можно применить генетический алгоритм для аппроксимации изображений полигонами. Как и в своих предыдущих статьях, использовать для этой цели я буду собственный фреймворк EvoJ, о котором уже писал здесь и здесь.

Выбор способа описания решения
Следуя традиционному пути решения задач при помощи EvoJ, для начала выберем как мы опишем решения для нашей задачи. Прямолинейным решением будет описать аппроксимацию как простой список полигонов:
public interface PolyImage {
List<Polygon> getCells();
}
Такой подход имеет право на жизнь, нам вполне удастся подобрать удовлетворительную картинку рано или поздно. Cкорее всего поздно, так как такой подход снижает эффективность скрещивания хороших решений. И вот почему.
Представим для простоты следующую картинку.

Допустим у нас в генофонде есть два хороших решения, каждое из которых отличается от идеального на один полигон.

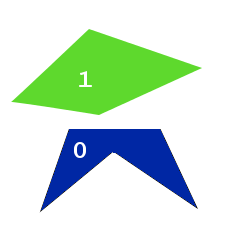
Обратите внимание на одну особенность: в обоих случаях полигон номер 0 идеально совпадает с одним из полигонов изображения, тогда когда другой лежит где-то в стороне. Был бы здорово скрестить эти два решения таким образом, чтобы в результате вместе оказались два первых полигона из обоих решений, однако это не возможно — EvoJ отображает все переменные на байтовый массив и при скрещивании работает с байтами, не меняя порядка их следования.
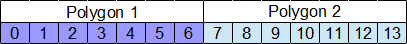
Процесс кроссинговера разъясняется на следующем рисунке.

Таким образом два элемента с одинаковым индексом никак не могут оказаться в результирующем решении.
Результат скрещивания скорее всего будет выглядеть так:

Что сильно скажется на эффективности скрещивания, значительно замедлив эволюцию.
Обойти проблему можно, «правильно» засеяв исходную популяцию — равномерно распределив полигоны по области изображения, таким образом, чтобы расположение полигона в списке, согласовывалось с его геометрическим расположением на рисунке. При этом придется ограничить мутацию, чтобы полигоны не могли слишком далеко «переползти».
Более продвинутый подход заключается в изначальном разделении изображения на ячейки, с назначением каждой ячейке собственного списка полигонов. В виде интерфейса Java это описывается так:
public interface PolyImage {
Colour getBkColor();
List<List<List<Polygon>>> getCells();
}
Внешний список задает ряды ячеек, следующий по вложенности — столбцы, и, наконец, внутренний список — полигоны находящиеся в в соответствующей ячейке. Такой подход автоматически обеспечивает примерное соответствие положения полигона в байтовом массиве и его геометрического места на рисунке.
Каждый полигон опишем как:
public interface Polygon {
List<Point> getPoints();
Colour getColor();
int getOrder();
}
Здесь свойство order определяет глобальный порядок отрисовки полигона. Цвет полигона опишем как:
public interface Colour {
@MutationRange("0.2")
@Range(min = "0", max = "1", strict = "true")
float getRed();
@MutationRange("0.2")
@Range(min = "0", max = "1", strict = "true")
float getGreen();
@MutationRange("0.2")
@Range(min = "0", max = "1", strict = "true")
float getBlue();
void setRed(float red);
void setGreen(float green);
void setBlue(float blue);
}
Иными словами, просто как три компоненты цвета, желающие еще могут добавить альфа-канал, однако мы будем рисовать все полигоны с 50% прозрачностью, это снизит число безразличных мутаций. Назначение аннотаций здесь, я надеюсь, очевидно. Если нет — загляните в мои предыдущие статьи, там этот вопрос разбирается.
Точки полигона опишем как:
public interface Point {
int getX();
int getY();
}
При этом координаты X и Y будем считать относительно центра ячейки, которой принадлежит полигон. Обратите внимание, что аннотации регулирующие допустимые значения переменных присутствуют только в описании цвета. Это связано с тем, что допустимые значения координат зависят от размера изображения и от конфигурации ячеек, а допустимые значения компоненты цвета — вещи предопределенные. Кроме того, аннотацию на два внутренних списка в интерфейсе PolyImage вообще никак повесить нельзя.
Чтобы задать все необходимые параметры мы воспользуемся механизмом под названием Detached Annotations.
Итак, перейдем к программированию. Исходники, используемые в данном примере могут быть найдены здесь. Многое из приведенного кода повторяет написанное в моих предыдущих статьях, многое не имеет отношение к генетическому алгоритму как таковому. По этому я заострю внимание на ключевых моментах, а остальные части прокомментированы в коде.
Кофигурирование EvoJ при помощи Detached Annotations
final HashMap<String, String> context = new HashMap<String, String>();
context.put("cells@Length", ROWS.toString());
context.put("cells.item@Length", COLUMNS.toString());
context.put("cells.item.item@Length", POLYGONS_PER_CELL.toString());
context.put("cells.item.item.item.points@Length", "6");
context.put("cells.item.item.item.points.item.x@StrictRange", "true");
context.put("cells.item.item.item.points.item.x@Min", String.valueOf(-widthRadius));
context.put("cells.item.item.item.points.item.x@Max", String.valueOf(widthRadius));
context.put("cells.item.item.item.points.item.x@MutationRange", "20");
context.put("cells.item.item.item.points.item.y@StrictRange", "true");
context.put("cells.item.item.item.points.item.y@Min", String.valueOf(-heightRadius));
context.put("cells.item.item.item.points.item.y@Max", String.valueOf(heightRadius));
context.put("cells.item.item.item.points.item.y@MutationRange", "20");
context.put("cells.item.item.item.order@Min", "0");
context.put("cells.item.item.item.order@Max", "1000");
Здесь мы создаем контекст — Map похожий на properties файл, где имя свойства соответствует пути к свойству объекта в нотации похожей на принятую в BeanUtils, за исключением того, что элементы списка обозначаются ключевым словом item.
Таким образом, имя cells описывает свойство cells нашего корневого интерфейса PolyImage. А строчка cells.item – элементы этого списка, которые в свою очередь являются списками описываемыми строчкой cells.item.item, итд.
После имени свойства и знака @ указывается имя detached аннотации, которое похоже на имя обычной аннотации. Обязательным является указание длины списка, чтобы EvoJ знала сколько места резервировать в байтовом массиве.
Аннотация cells.item.item.item.points@Length задает количество точек в полигоне (проследите путь — свойство cells, три вложенных списка, свойство points у элементов самого вложенного списка.
Схожим образом задаются границы значений координат точек, радиус их мутации, пределы значений свойства order.
Далее мы используем заполненный контекст при создании генофонда.
Создание фитнес функции
В качестве фитнес-функции выберем сумму квадратов отклонений подбираемого изображения от оригинального, со знаком минус — так как наилучшим решениям соответствует наименьшая сумма. Фитнес-функция имплементирована в классе ImageRating, остановимся на его ключевых моментах.
Как и в примерах из предыдущих статей, класс наследуется от helper-класса AbstractSimpleRating:
public class ImageRating extends AbstractSimpleRating<PolyImage>
и имплементирует абстрактный метод doCalcRating следующим образом:
@Override
protected Comparable doCalcRating(PolyImage solution) {
BufferedImage tmp = drawImage(solution);
return compareImages(originalImage, tmp);
}
Здесь функция drawImage тривиально отрисовывает все полигоны в соответствии с их ячейкой, порядком, цветом, итд. Не будем подробно на ней останавливаться — ничего относящегося к генетическому алгоритму в ней не содержится.
Функция же compareImages осуществляет попиксельное сравнение изображений. Рассмотрим ее чуть ближе
private Comparable compareImages(BufferedImage originalImage, BufferedImage tmp) {
long result = 0;
int[] originalPixels = originalImage.getRaster().getPixels(0, 0, originalImage.getWidth(), originalImage.getHeight(), (int[]) null);
int[] tmpPixels = tmp.getRaster().getPixels(0, 0, tmp.getWidth(), tmp.getHeight(), (int[]) null);
for (int i = 0; i < originalPixels.length; i++) {
long d = originalPixels[i] - tmpPixels[i];
result -= d * d;
}
return result;
}
Как видно, функция довольно тривиальна — она берет растры оригинального и свеженарисованного изображений и сравнивает их поэлементно, попутно складывая (со знаком минус) квадраты разниц.
Осуществление итераций
Для того, чтобы быстрее достичь результата необходимо выбрать оптимальные параметры мутации:
- вероятность того что решении вообще подвергнется мутации
- вероятность мутации каждой переменной внутри решения
- радиус изменения — максимальное расстояние на которое может сместиться точка в ходе мутации
- срок жизни решения (не совсем относится к мутации, но так же влияет на скорость сходимости)
Выбор стратегии — дело не тривиальное. С одной стороны, сильная мутация позволяет быстрее охватить пространство решений и «нащупать» глобальный экстремум, но с другой стороны не позволяет в него скатиться — решения будут его постоянно проскакивать. Долгий срок жизни решения страхует от ухудшения значения фитнес функции, но замедляет общий прогресс и способствует скатыванию в локальный экстремум вместо глобального. Еще нужно решить, что нужно мутировать с большей вероятностью — точки полигонов или их цвета.
Кроме того, выбранная стратегия через некоторое время себя исчерпывает — найденные решения начинают колебаться вокруг найденного экстремума, вместо того чтобы в него скатиться. Чтобы справиться с этой проблемой, стратегии надо менять. Генеральная идея при этом заключается в том, чтобы уровень мутации со временем уменьшался, а время жизни удачных решений росло. Стратегии мутации, использованные в примере, подобраны эмпирическим путем.
Учитывая все выше написанное, главный цикл программы устроен следующим образом:
- произвести 10 итерации генетического алгоритма
- взять значение фитнес-функции у наилучшего решения
- определить не пришла ли пора менять стратегию
- изменить стратегию, если необходимо
- сохранить картинку во временный файл
- обновить UI
Запустив программу, минут через 15 (в зависимости от мощности вашей машины) вы обнаружите, что подобранное изображение уже отдаленно напоминает оригинал, а через час-два вы достигнете результата близкого к тому, что приведен в начале статьи.
Дальнейшее улучшение алгоритма
Прогресс можно значительно ускорить применив следующие оптимизации:
- аппроксимацию производить в пространстве Lab вместо RGB, оно характеризуется тем, что декартово расстояние между точками в цветовом пространстве примерно согласуется с воспринимаемой глазом разницей. Количества итераций в секунду это не добавит, зато направит эволюцию в нужном направлении.
- создать маску важности областей изображения — черно-белое изображение с выделенными областями интереса, которое затем использовать при расчете фитнес-функции, это позволит сконцентрировать эволюцию на том, что действительно представляет интерес.
- для изображений использовать VolatileImage. На моей машине рисование на VolatileImage в 10 раз быстрее чем рисование на BufferedImage. Правда, потом результат приходится все равно конвертировать в BufferedImage, чтобы получить цвета пикселей, это приводит к существенному падению быстродействия, но все равно окончательный результат в 3 раза лучше, чем просто рисовать полигоны на BufferedImage.
- подобрать оптимальные параметры мутации на разных этапах. Задача это не простая, но и тут может помочь генетический алгоритм. Я проводил эксперименты, где переменными были параметры мутации, а фитнес-функцией — средняя скорость уменьшения ошибки за 100 итераций. Результаты обнадеживают, однако для решения этой задачи требуется значительная вычислительная мощность. Возможно я в одной из следующих статей я разберу это проблему ближе.
- завести несколько независимых генофондов и производить эволюцию в них независимо, через определенные промежутки времени скрещивать между собой особей из разных генофондов. Такой подход называют островной моделью ГА, т. е. эволюция как бы протекает на изолированных друг от друга островах, скрещивания между особями с разных островов крайне редки.
- засевать изображение полигонами постепенно: сначала поместить по 1-2 полигона в каждую ячейку, позволить им «расползтись», затем добавить еще по 1-2 полигона в места, где наблюдается наибольшее отклонение изображения от оригинала и подвергать эволюции только вновь добавленные полигоны, так повторять пока не будет достигнут предел числа полигонов в ячейке, после чего запустить эволюцию по всему изображению, как описано в статье выше. Такой подход приводит к наиболее точным близким аппроксиммациям.
Послесловие
Итак, мы рассмотрели пример, как можно применить EvoJ для решения задачи аппроксиммации изображения. Стоит отметить, что аппроксимация изображений генетическим алгоритмом представляет собой скорее академический или эстетический интерес нежели практический, ибо подобного результата можно добиться другими, специально заточенными алгоритмами векторизации изображений.
В следующий раз я расскажу о применении генетического алгоритма для генерации дизайнерских идей.
Автор: tsvetkovpa






