I. Предисловие.
Когда-то давно мне запал в память эпизод из киберпанковского романа: один герой показывает другому экран, на котором быстро сменяют друг друга пиксели. Каждое состояние экрана представлено определённым числом, программа постепенно перебирает варианты.
Можно представить, что рано или поздно на таком экране могли бы появиться разные удивительные вещи: страница из «Войны и мира», «Джоконда», первые такты «Лунной сонаты», гениальное решение известного уравнения, фотография любого человека, эта страница Хабра, сообщение о безвестном событии прошлого или подробное предсказание будущего.
С тех пор я периодически пытался сделать что-то по касательной, были какие-то мелкие поделки на Perl. А недавно захотелось сделать что-то подобное на JavaScript.
II. Условия реализации.
Реализовать такой перебор и его графическое отображение несложно. Вот только доступные масштабы будут совсем невелики.
Допустим для простоты, что каждая точка экрана представлена двумя состояниями — белым и чёрным цветом, что отвечает нулю и единице в бинарном представлении числа. Последовательные координаты точек отвечают порядковому месту цифры в числе.
На данный момент в JavaScript максимальное целое число с сохранением точности вычислений — 2 в степени 53. Math.pow(2,53) == Math.pow(2,53) + 1 даёт true. Это число представлено 54-мя бинарными позициями:
0b100000000000000000000000000000000000000000000000000000
0x20000000000000
9007199254740992Числу будет отвечать матрица всего 9 на 6 пикселей. Допустим, мой компьютер может совершать около 50 миллионов операций в секунду. Чтобы перебрать все варианты матрицы ему понадобится по грубым подсчётам
Math.pow(2,53) / 50000000 / 60 / 60 / 24 / 365 — около шести лет.
Более сильному компьютеру понадобится меньше, но перебор с такой предельной скоростью не сможет анализировать человек. Допустим, состояния матрицы будут сменять друг друга с традиционной частотой телетрансляции — 25 кадров в секунду. Тогда, чтобы перебрать с визуальной скоростью все состояния крошечного кусочка двухмерной чёрно-белой реальности, нам понадобится 1 428 082 года.
И всё же интересно создать что-то подобное. Упомянутое максимальное число для этого не очень удобно, потому что, когда левая верхняя точка становится единицей (перекрашивается в чёрный цвет), больше на этой матрице уже ничего не нарисуешь. Поэтому мы никогда не сможем полностью использовать крайние верхние и левые линии в нашей микрографике. Поэтом возьмём чуть меньшее число, матрица которого может быть полностью заполнена чёрным цветом, может принимать действительно любые состояния и иметь относительно пропорциональную форму. Это будет матрица 10 на 5 с максимальным числом в 50 двоичных порядков:
parseInt(
"1111111111" +
"1111111111" +
"1111111111" +
"1111111111" +
"1111111111"
, 2)0b11111111111111111111111111111111111111111111111111
0x3ffffffffffff
1125899906842623Все дальнейшие реализации успешно тестировались на последних версиях Chrome, Firefox, Opera и Safari. К сожалению, на IE я протестировать не смог, но большинство примеров точно не будут работать на версиях по восьмую включительно.
Любую матрицу можно сохранить, подредактировать при необходимости код и запускать локально.
Понимаю, что всё дальнейшее похоже на детский сад. Поэтому прошу снисхождения к человеку с гуманитарным складом ума, пытающемуся играть чужими игрушками. Всё это just for (slightly metaphysical) fun :)
III. Последовательная матрица.
Поскольку матрица очень маленькая, реализовывать её на пиксельной графике не очень удобно и наглядно, поэтому для простоты и удобства масштабирования у нас будет простая таблица 10 на 5 ячеек с изменяющимся цветом. Первый порядок находится в нижнем правом углу.
Для начала я написал конвертер графики в число для такой матрицы. Каждое нажатие мышки на ячейке изменяет цвет и соответственно переключает порядок в числе между единицей и нулём. Над табличкой отображается само число в десятичном формате. Размер ячейки в пикселях можно задавать параметром scale в адресе страницы.
Осталось написать саму матрицу с последовательной сменой состояний. Это будет всё та же таблица, но с другим поведением. Чтобы ничего не отвлекало на странице от чистоты представления, управление в этой и следующих поделках распределится между мышкой и параметрами в URL.
У нашей матрицы три параметра со следующими умолчаниями:
scale=10 — уже упомянутый размер ячейки в пикселях;
fps=25 — частота смены кадров в секунду;
start=1 — число, с которого начинается перебор.
Каждый щелчок мышки увеличивает число на единицу и изменяет состояние матрицы. Если щёлкнуть с нажатой клавишей Ctrl, запускается/останавливается автоматический перебор. Текущее число отображается в заголовке документа (окна, вкладки).
Скажем, между состоянием, отображающим графическую единицу:

и состоянием, отображающим графическую двойку:

проходит 7697662480391 - 1100586419201 = 6597076061190 кадров. При FPS по умолчанию это около 8368 лет созерцания :)
Чем выше и левее находится точка, тем больше времени проходит до её появления.
Можно, например, посмотреть, как главный ответ на главный вопрос превращается понемногу в какой-нибудь другой ответ.
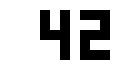
IV. Случайные матрицы.
1. Одно число.
Нашу матрицу последовательного перебора можно переделать в матрицу, перебирающую случайные значения. Параметр начального числа теряет свой смысл, в остальном всё остаётся по-прежнему (разве что частоту кадров по умолчанию мы снизили до 1 в секунду, иначе выходит неразборчивое мельтешение).
Одно из случайных состояний, как ни странно — с совершенной буквой А:

2. Множества чисел.
Чтобы как-то разнообразить нашу матричную действительность, выйдем за границы перебора одного числа. Будем создавать матрицы, не ограниченные в размере. Состояния их будут задаваться множеством случайных чисел по разным принципам. Реализовывать их будем при помощи canvas.
а. Случайные цельные изображения.
Тут каждый кадр матрицы будет совершенно отличен от другого. Каждая точка кадра задаётся одним случайным числом. Разберём параметры по умолчанию (прежние и будущие ссылки включают эти параметры для наглядности: эти настройки используются, если никаких параметров не задавать).
w=400 — ширина матрицы в пикселях
h=300 — высота матрицы в пикселях
fps=1 — частота смены кадров
Как и ранее, один щелчок мышки сменяет один кадр. Щелчок с клавишей Ctrl запускает смену случайных состояний. Но теперь прибавляются ещё некоторые возможности.
При нажатии средней кнопки мышки в новой вкладке или в новом окне открывается копия матрицы в формате PNG, если вдруг зачем-то нужно сохранить картинку (кстати, все последующие иллюстрации получены именно так).
Щелчок левой кнопки с нажатой клавишей Shift переключает глубину цвета картинки: чёрно-белый режим, оттенки серого, цветной режим. Если зажать клавиши Shift+Alt, переключение производится в обратном порядке.
Конечно, случайность каждой точки означает, что в подавляющем большинстве состояний мы получим графический шум вроде экрана ненастроенного телевизора. Ведь чередования распределяются на таком пространстве относительно равномерно. Однако люди с богатой фантазией и чутким восприятием могут усмотреть в этом шуме интересные сюжеты или неожиданно вспомнить о чём-то волнующем из-за прихотливых ассоциаций.
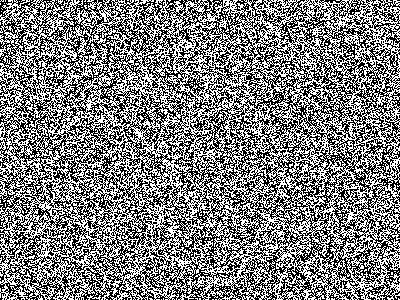


б. Случайные точки.
В этом виде матрицы к постоянному фону последовательно добавляются случайные точки. Введём ещё один параметр:
bg=w — цвет фона (w — белый (white), b — чёрный (black)). Также добавляется ещё один цветовой режим, их теперь четыре: одноцветный (чёрные или белые точки на противоположном фоне; рано или поздно они могут заполнить весь холст и состояние перестанет наглядно меняться) и прежние три режима (в них заполнения не происходит, поскольку даже в минимальном чёрно-белом режиме прежнее состояние может закрашиваться новым).
Появляющиеся на чёрном фоне точки в режиме оттенков серого или цветном похожи на зажигающиеся звёзды разной яркости.

А если фон сделать белым, запустить анимацию и увеличить масштаб страницы, со временем можно будет поиграть в игру, часто встречающуюся в детских журналах: соедини точки, чтобы получилась картинка. Правда картинка не будет заранее известной.
в. Случайные линии.
В этом виде матрицы к фону постоянно добавляются случайные линии. Помню, в школе мы часто играли в другую похожую игру: берётся чистый лист, один игрок рисует на нём не глядя произвольный узор, потом по очереди остальные игроки другим цветом обводят увиденные ими образы. На нашей матрице появляются узоры, похожие на начальные поля этой игры.
К прежним факторам случайности (координаты точек и цвет) добавляются ещё два. За них отвечают новые параметры:
lines=r — вид линий (может принимать три значения: s — только прямые (straight), c — только кривые (curve), r — случайное чередование прямых и кривых (random); при черчении кривых к двум случайным точкам начала и конца отрезка добавляются ещё две случайные точки, управляющие изгибом — обычные параметры для кривых Безье);
traverse=r — способ рисования (тоже принимает три значения: y — рисовать, не отрывая руку от бумаги (yes), n — каждый раз начинать линию с новой случайной точки (no), r — случайное чередование отрыва с безотрывным продолжением (random)).
Прежние четыре цветовых режима остаются и здесь.


г. Случайные фигуры.
Теперь мы будем замыкать линии и закрашивать их. Будут получаться как бы случайные «мазки». Параметр traverse теряет свой смысл, зато добавляются новые три фактора случайности со своими параметрами.
alpha=y — случайно менять уровень прозрачности цвета (два значения, y (yes) или n (no), соответственно использовать прозрачность или нет). При использовании прозрачности первые три режима глубины цвета (одноцветный, чёрно-белый и оттенками серого) становятся очень похожими друг на друга.
minnodes=3 — минимальное количество узлов в фигуре
maxnodes=10 — максимальное количество узлов в фигуре.
По умолчанию установлены ограничения от 3 (меньше устанавливать нет смысла, потому что фигуры не получится) до 10 (это верхнее ограничение можно отредактировать в коде). На форму фигур также большое влияние оказывает уже описанный параметр lines (получаются соответственно многоугольники или более сложные формы). Следует учитывать, что фигуры часто будут самопересекающимися, поэтому заливка будет сложной, с разнообразными пробелами.
Далее следуют примеры разных цветовых режимов на разном фоне, с использованием прозрачности и без использования альфа-канала.






Можно также соединить все описанные виды рисования (фрагменты цельных изображений, точки, линии, фигуры). Эту игру с кодом я предоставляю заинтересовавшимся. Искреннее спасибо всем за внимание :)
Ссылки на все описанные матрицы.
Автор: vmb

