
В моей статье полугодичной давности о длинной арифметике есть замеры скорости (throughput в тактах) очень коротких фрагментов кода — всего по несколько инструкций. Методика измерения была кривовата, но давала правдоподобные результаты. Потом выяснилось, что результаты таки неверные — поверхностный подход всегда сказывается.
В этом посте я опишу надежный метод «нанобенчмаркинга» с минимальной погрешностью и без подключения специальных библиотек и драйверов, к которому в итоге пришел. Применимость: сравнение однопоточного потенциала процессоров, просто интерес.
Я использую только GCC — соответственно способ заточен под него. Но буду делать обобщения, чтобы владельцы других компиляторов могли разобраться.
Непосредственно мерилом служит команда RDTSC. На Википедии справедливо отмечается, что она ненадежна и рекомендуется использовать специальные сервисы ОС. Однако для микроизмерений они работают слишком долго (сотни тактов) и неодинаково от запуска к запуску, что вносит неустранимые погрешности. Сама по себе RDTSC работает не более нескольких десятков тактов — постоянное количество или одно из небольшого набора.
Единственным недостатком RDTSC при микроизмерениях остается плавающая тактовая частота процессоров, потому что time stamp counter всегда считает такты в соответствии со стандартным множителем. Зафиксировать множитель — задача не всегда тривиальная, ищите "disable cpu scaling" в сочетании с названием своей ОС и типом процессора. Удачное решение в Gnome — апплет indicator-cpufreq.
Измерительная обвязка состоит из трех вложенных циклов.
Внутренний цикл управляет потоком данных как и в рабочей программе.
В таком духе:
type input1[n];
type input2[n];
type output[n];
...
for (int i = 0; i < n; i++) {
обработать input1[i] и input2[i]
результат записать в output[i]
}
Важно, что в фразе «померить код» под «кодом» в этой статье подразумевается определенная последовательность инструкций процессора. Поэтому часть цикла между скобками либо должна быть написана на ассемблере, либо на Си, но вы должны четко понимать, чего добиваетесь от компилятора. Чтобы побороть кипучую активность GCC при -O3, сразу добавьте опции -fno-prefetch-loop-arrays, -fno-unroll-loops, -ftree-vectorizer-verbose=1. -fno-tree-vectorize либо -ftree-vectorize — уже в зависимости от того, что требуется на выходе — «как написано» или векторизованный вариант цикла.
Если вы хотите измерить обработку конкретного входа или код вообще без входа/выхода, все равно заверните его в цикл. Чтобы GCC не вынес код обратно, включите -fno-gcse (global common subexpression elimination), -fno-tree-pta (points-to analysis) и -fno-tree-pre (partial redundancy elimination). См. все опции оптимизации.
Начало цикла выровняйте на 32 байта. При -falign-loops (-O2) GCC делает это сам.
Средний цикл содержит 2 замера тактов и неизменный внутренний цикл посередине. Его роль — определить минимальное время, за которое может выполниться внутренний цикл. 20-30 итераций вполне хватает, чтобы все данные попали в кеш, начальная и конечная RDTSC заняли одинаковое время, а также сошлись все прочие звезды, если они существуют :-)
Внешний цикл управляет длиной внутреннего. Расположите в нем инициализацию входных данных перед средним циклом.
Внешний цикл необходим, потому что время, достигнутое в среднем цикле, всегда включает константу — время инициализации внутреннего цикла + затраты на 1 ошибку в предсказании перехода (самые умные интеловские ядра ошибаются реже). Поэтому время из среднего цикла нельзя просто разделить на кол-во итераций.
Но даже это еще не все! Разница времени выполнения внутренних циклов, отличающихся по длине на 1 итерацию, зачастую существенно варьируется. Причина — влияние разных этапов конвейера друг на друга. В то время, когда на каком-то этапе по идее должна вестись работа, на самом деле может происходить следующее:
- обработка данных,
- простой, т. к. следующий этап еще занят,
- простой, т. к. не пришли данные с предыдущего этапа.
Кроме того, некоторые этапы имеют необычное поведение, например предсказатель переходов и планировщик микроопераций. Все это порождает затейливые эффекты.
В итоге на конвейере устанавливается «паттерн» работы длиной от 1 до 10-15(?) итераций:
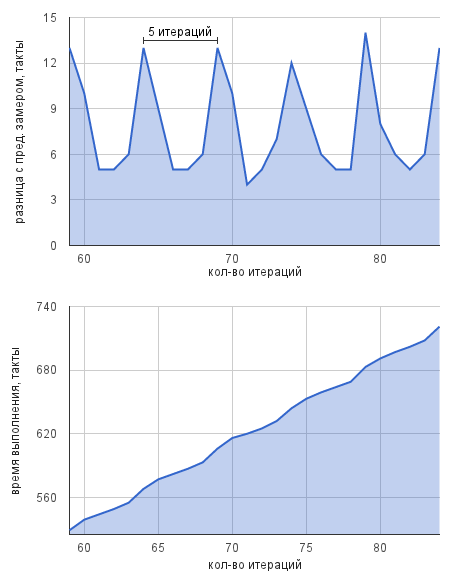
Точный througput в тактах имеет смысл считать как минимум для 1 такого паттерна, а не 1 итерации.
Как легко убедиться из цифр в примерах ниже, даже при измерении паттернов разброс результатов остается. Предположительно, на самом деле RDTSC не так хороша, как расписано выше :-)
Итак, получив разницы времени выполнения внутренних циклов с длинами кратными шагу паттерна, остается посчитать статистики.
Примеры
Сравните результаты замеров (здесь и далее все значения в тактах) из статьи про длинную арифметику:
| Поверхностный метод | 7.5 | 5.5 | 5.5 | 7 | 5 | 2 | 2.5 | 3.25(?)–3.5 |
| Умный метод | 7 | 6 | 6 | 7 | 5 | 2 | 2 | 3 |
Все дальнейшие тесты проводились на 2 ядрах: AMD K10 и Intel Core 2 Wolfdale.
Важно оценить сами инструменты.
Пустой цикл
Внутренний цикл выглядит так:
for (int i = 0; i < inner_len; i++) {
asm volatile ( "" );
}
K10 1.8 ± 0.7 Core 2 10.0 ± 2.4 на 10 итераций.
Далее (10, 1.0) — (длина паттерна, итого в среднем на 1 итерацию)
RDTSC
Без среднего и внутреннего цикла:
typedef unsigned long long ull;
inline ull rdtsc() {
unsigned int lo, hi;
asm volatile ( "rdtscn" : "=a" (lo), "=d" (hi) );
return ((ull)hi << 32) | lo;
}
...
for (int i = 0; i < TOTAL_VALUES; i++) {
ull t1 = rdtsc();
ull t2 = rdtsc();
printf("%lldn", t2 - t1);
}
K10 69.7 ± 1.5 Core 2 31.0 ± 0.3
Приближенное вычисление синуса
Интересно посмотреть, сколько можно сэкономить, вычисляя синус рядом Тейлора 3-го порядка. При углах от −π/2 до π/2 получается точность в 2 знака после запятой. Можно представить приложения, где ее будет достаточно.
Каркас:
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <limits>
typedef unsigned long long ull;
#define MIDDLE_LEN (20)
#define TOTAL_VALUES (10000)
#define VEC_LEN (1)
// len in _numbers_
#define DATA_LEN (TOTAL_VALUES * VEC_LEN)
inline ull rdtsc() {
unsigned int lo, hi;
asm volatile ( "rdtscn" : "=a" (lo), "=d" (hi) );
return ((ull)hi << 32) | lo;
}
typedef double my_float;
#define BYTE_LEN (DATA_LEN * sizeof(my_float))
int main() {
my_float* angles = (my_float *) malloc(BYTE_LEN);
my_float* sines = (my_float *) malloc(BYTE_LEN);
еще приготовления
for (int inner_len = 0; inner_len < DATA_LEN; inner_len += VEC_LEN) {
for (int i = 0; i < inner_len; i++)
инициализация angles[i]
ull inner_min = std::numeric_limits<ull>::max();
for (int mi = 0; mi < MIDDLE_LEN; mi++) {
ull t1 = rdtsc();
for (int i = 0; i < inner_len; i += VEC_LEN) {
записать синус angles[i] в sines[i]
}
ull t = rdtsc() - t1;
inner_min = t < inner_min ? t : inner_min;
}
// статистики считаются отдельным скриптом
printf("%lldn", inner_min);
}
}
Инструкция FSIN — точный синус
Именно ее вызывает sin из math.h. Генерируемые микрооперации, наверное, напоминают эту реализацию синуса, так как скорость выполнения тоже зависит от угла. Поэтому точный througput имеет смысл, если в цикле вычисляется синус одного и того же угла. Среднее по случайному углу нужно для сравнения с независимым от угла грубым расчетом.
// приготовления
my_float randoms[DATA_LEN];
for (int i = 0; i < DATA_LEN; i++)
randoms[i] = rand() / 2.0 / RAND_MAX * M_PI;
// инициализация углов
angles[i] = 0.0 или 0.0001 или M_PI * 0.5 или randoms[i];
// вычисление синуса
asm volatile (
"fldl (%0)nt"
"fsinnt"
"fstpl (%1)nt"
:: "r" (angles + i), "r" (sines + i)
);
| угол | 0.0 | 0.0001 | π/2 | случайный |
| K10 | 30.2 ± 10.3 | 89.8 ± 2.9 | 143.1 ± 8.5 (2, 71.6) | 75.6 |
| Core 2 | 40.0 ± 11.0 | 68.0 ± 5.6 | 88.0 ± 13.0 | 89.4 |
Ряд Тейлора 3-го порядка
// приготовления
my_float d6 = 1.0 / 6.0;
my_float d120 = 1.0 / 120.0;
my_float randoms[DATA_LEN];
for (int i = 0; i < DATA_LEN; i++)
randoms[i] = rand() / 2.0 / RAND_MAX * M_PI;
// инициализация углов
angles[i] = randoms[i];
// вычисление синуса
my_float x = angles[i];
sines[i] = x - x*x*x*d6 + x*x*x*x*x*d120;
| K10 | 61.2 ± 15.6 (8, 7.7) |
| Core 2 | 35.2 ± 16.8 (4, 8.8) |
Векторизованный ряд Тейлора
Если просто добавить опцию GCC -ftree-vectorize, по сути будет тот же результат (cм. выше). А тут используются Vector Extensions.
#define VEC_LEN (2)
typedef my_float float_vector __attribute__ ((vector_size (16)));
...
// приготовления
float_vector d6_v = {1.0 / 6.0, 1.0 / 6.0};
float_vector d120_v = {1.0 / 120.0, 1.0 / 120.0};
my_float randoms[DATA_LEN];
for (int i = 0; i < DATA_LEN; i++)
randoms[i] = rand() / 2.0 / RAND_MAX * M_PI;
// инициализация углов
angles[i] = randoms[i];
// вычисление синуса
float_vector x = *((float_vector *)(angles + i));
*((float_vector *)(sines + i)) = x - x*x*x*d6_v + x*x*x*x*x*d120_v;
| K10 | 41.8 ± 14.2 (5, 8.4, 4.2 на 1 синус) |
| Core 2 | 44.3 ± 16.6 (5, 8.9, 4.5) |
Скорость выполнения 1 итерации чуть ниже, чем в скалярном варианте, а вычисления синуса 1 угла — почти в 2 раза выше.
Получается, что вычисление синуса с точностью до 2 знаков можно организовать как минимум в 10 раз быстрее, чем обычно.
Источники
Еще ссылки
П. С.
Описанный метод не профилирует код. Вероятность того, что он поможет при оптимизации, также крайне мала, потому даже если производительность упирается в вычислительный конвейер, сравнивать решения всегда можно обычным clock()-ом по циклу на миллион итераций.
Автор: leventov






