В предыдущей статье я рассказал, как симметричные карты позволяют достаточно просто и быстро минимизировать булевые функции, но не осветил два момента: получение разных вариантов минимального решения и автоматизацию самого алгоритма минимизации. Расскажу здесь об этом более подробно.
Напомню, что задача минимизации — для каждой единицы найти наибольшее покрытие. Если такое покрытие найдено и оно единственное, то оно записывается в так называемое ядро функции, а все единицы, им покрываемые выбывают из дальнейшего рассмотрения. Однако, если максимальное покрытие не единственное, возникают варианты решения, которые возможно использовать, например, для учета каких-либо дополнительных требований. Кроме того, как я покажу далее, отбрасывание вариантов приводит к тому, что полученное решение может оказаться не минимальным.
Итак, в примере из предыдущей статьи, можно найти ядро функции для следующей симметричной карты:
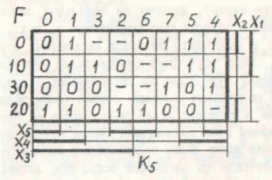
Оно равно:
!X1*X5 V X2*X3*X4 V X1*!X2*!X5
Можно найти, что единица в строке с индексом 0 и столбце с индексом 4 может быть покрыта двумя способами:
!X1*X3*!X4 (1)
X3*!X4*!X5 (2)
Аналогично, единица в строке с индексом 10 и столбце с индексом 4 может быть покрыта четыремя способами:
!X1*X3*!X4 (1)
X3*!X4*!X5 (2)
!X1*X2*X3 (3)
X2*X3*!X5 (4)
Заметим, что при покрытии разных единиц встречаются одинаковые импликанты, обозначенные здесь одинаковыми цифрами.
Далее, единица в строке с индексом 30 и столбце с индексом 4 может быть покрыта тремя способами:
X3*!X4*!X5 (2)
X1*X3*!X5 (5)
X2*X3*!X5 (4)
И единица в строке с индексом 20 и столбце с индексом 1 может быть покрыта двумя способами:
X1*!X2*!X3*!X4 (6)
!X2*!X3*!X4*X5 (7)
Поскольку в окончательном решении должны быть покрыты все единицы, запишем следующее выражение в виде произведения вариантов для каждой единицы:
(1 V 2)(1 V 2 V 3 V 4)(2 V 5 V 4)(6 V 7)
Раскроем первые две скобки:
(1*1 V 1*2 V 1*3 V 1*4 V 2*1 V 2*2 V 2*3 V 2*4)(2 V 5 V 4)(6 V 7)
Поскольку импликанта, будучи умноженная сама на себя дает ту же импликанту, первую скобку можно переписать в следующем виде:
(1 V 1*2 V 1*3 V 1*4 V 2*1 V 2 V 2*3 V 2*4)(2 V 5 V 4)(6 V 7)
Далее, поскольку вариант с одной импликантой дает лучшее решение, чем с двумя, можно переписать решение в виде:
(1 V 2)(2 V 5 V 4)(6 V 7)
Раскрывая скобки далее и используя подобные сокращения, получаем окончательное решение, которое уже нельзя сократить:
2(6 V 7)
Первый множитель 2 — единственная импликанта в группе и должна быть довавлена в ядро функции (так называемое расширенное ядро функции):
X3*!X4*!X5
А скобка дает два варианта:
X1*!X2*!X3*!X4
и
!X2*!X3*!X4*X5
Можно выбрать любой из них.
Естественно, возникает вопрос про автоматизацию данного алгоритма. Для этого мной была написана программа apssymmap, которую можно найти на моем сайте:
http://andyplekhanov.narod.ru/soft/soft.htm
Представляет интерес сравнить результаты применения данного метода с другими известными методами. Сравним результаты работы программы apssymmap с известной программой espresso на примере, представленном ниже:
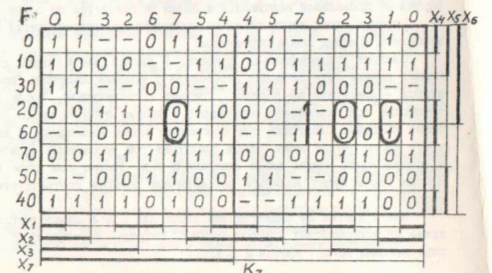
Результат работы программы espresso:
espresso -Dexact -oeqntott test.txt

Результат работы программа apssymmap:

Видно, что программа apssymmap выдает 8 различных вариантов вместо одного у espresso. Однако, более интересным фактом является то, что результат espresso не является оптимальным. Если отбросить все общие части в этих решениях, можно увидеть, что у espresso останется две импликанты:
!X7*!X5*!X4*X2*X1
и
X7*!X6*X5*X4*X3*X1
содержащие соответственно 5 и 6 переменных, а в решении apssymmap будут импликанты
!X5*X3*X2*X1
и
X7*!X6*X3*X2*X1
содержащие 4 и 5 переменных, то есть на две меньше. В качестве вывода можно сделать заключение, что симметричные карты являются не только более удобным методом при ручной минимизации булевых функций, но и превосходят другие методы при решении этой задачи на компьютере.
Автор: andy_p





