
Какая медлительная страна! — сказала Королева. — Ну, а здесь,
знаешь ли, приходится бежать со всех ног, чтобы только остаться
на том же месте! Если же хочешь попасть в другое место, тогда
нужно бежать по меньшей мере вдвое быстрее!
Льюис Кэрролл "Алиса в Зазеркалье"
Сегодня, я хочу рассказать об удивительной и недооценённой игре, с которой я познакомился чуть менее двух лет назад. В каком-то смысле, именно с этой игры, а также с Ура, началось моё знакомство с Дмитрием Скирюком. В те дни я только начинал интересоваться настольными играми. Мои познания были скудны и, во многом, наивны. Такие игры как "Чейз", буквально открыли для меня новый необъятный мир. Даже сейчас, работа над этой игрой, в большой степени, напоминает детективную историю. В этом отношении, игра "Chase" полностью оправдала как своё название так и сходство с псевдонимом известного американского писателя.
Игра была разработана Томом Крушевски и выпущена в продажу компанией «TSR» в 1986 году. Помимо специальной доски, у каждого из игроков имеется по 10 шестигранных игральных кубиков, но несмотря на это игра не является азартной. Кубики бросаются всего один раз, для определения очерёдности хода и в дальнейшем используются лишь в качестве фигур. Количество очков на верхней грани показывает число шагов, на которое может быть передвинут кубик. Так кубик с одним очком может быть перемещён на соседнее поле, в любом из шести направлений, с двумя очками — на два поля по прямой, с тремя — на три и т.д. Кубик должен перемещаться ровно на указанное число шагов, не больше и не меньше. В процессе перемещения, кубик не поворачивается другой стороной (количество очков на верхней грани не изменяется). Начальная расстановка показана ниже:

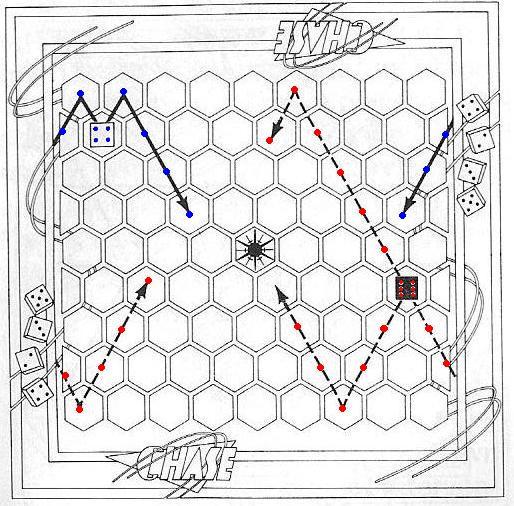
Границы доски не препятствуют движению фигур. Левая и правая границы доски «склеены» между собой, а от верхней и нижней границ фигуры отскакивают «рикошетом». Разумеется, это не означает, что фигуры движутся беспрепятственно. Фигуры не могут «перепрыгивать» друг друга, а также центральное поле "Chamber". Для взятия фигуры противника, фигура должна «встать» на неё (шахматное взятие), выполнив полное количество шагов по прямой. Ход может закончится и на фигуре своего цвета. В этом случае происходит "bumping" — фигура оказавшаяся на целевом поле смещается на один шаг, продолжая направление движения (с учётом склеенности доски и рикошетов). Если следующее поле также оказалось занято своей фигурой, "bumping" распространяется далее, до первого пустого поля или поля занятого фигурой противника (вражеская фигура забирается). Только одно препятствие может сделать такой ход невозможным — запрещено «задвигать» фигуры в центральную клетку, используя bumping.
Можно заметить, что из начальной позиции, каждый из игроков может циклически сдвинуть все свои фигуры, сходив любой из единичек в сторону двойки. Подобный ход разрешён правилами. Также допускается «обмен» очками между фигурами одного цвета, находящимися на соседних полях. Так пара из 5 и 2 может превратиться в 4 и 3 или даже в 1 и 6. Такое действие считается ходом. Не рассмотренным остался всего лишь один тип хода. Ни одна из фигур не может пройти сквозь центральное поле доски (Chamber), но она может закончить своё движение на этом поле. Если это произошло, фигура «расщепляется» на две, с сохранением суммарного количества очков. Фигура всегда разделяется таким образом, чтобы очки одной из полученных фигур превышали очки другой не более чем на 1. Общее количество фигур, у каждого из игроков, не может превысить 10 (именно на этот случай, в начале игры, каждый из игроков имеет 1 кубик в резерве).
Направления «разлёта» осколков напоминают остриё стрелы. Кубик с большим числом очков (если такой есть) всегда уходит в левую сторону. В двух особых случаях «расщепление» невозможно. Во первых, как я уже сказал выше, количество кубиков одного цвета не может превышать 10. Кроме того, совершенно очевидно, что расщепить кубик с 1 очком не удастся. В обоих этих случаях, кубик, вошедший в Chamber, выходит неизменным, по левому направлению. Каждая из фигур, покинувших Chamber, может инициировать bumping, попав на свою фигуру или взять фигуру противника (только таким способом можно взять две вражеских фигуры одновременно).
Должен сказать, что Tom Kruszewski и «TSR» сильно переоценили возможности своей потенциальной аудитории. Для массового потребителя, игра оказалась слишком сложной (шахматы не менее сложны, но к ним все привыкли). Производитель прекратил выпуск продукции и, в настоящее время, «Чейз» можно приобрести лишь с рук, на различных ярмарках, аукционах и распродажах. Тем не менее, эта игра по праву считается одной из лучших игр 20-го столетия.
Простая работа
Игра начинается с доски, а доска у Chase… своеобразная. Ранее мне ещё не приходилось делать игры на гексагональных досках и это стало первым (очень небольшим) препятствием. Это интересный момент и я хочу рассказать о нём поподробнее. Механизм описания игровых досок в ZRF хорошо продуман и позволяет реализовывать практически любые доски, при условии того, что они отображаются на плоскость и не изменяются в процессе игры.
(board
(image "../Images/Chase/board.bmp")
(grid
(start-rectangle 48 32 108 82)
(dimensions
("a/b/c/d/e/f/g/h/i/j/k/l/m" (60 0))
("1/2/3/4/5/6/7/8/9" (-30 52))
)
(directions (se 1 1) (w 1 0) (sw 0 1)
(nw -1 -1) (e -1 0) (ne 0 -1))
)
(kill-positions
j1 k1 l1 m1 j2 k2 l2 m2 a3 k3 l3 m3
a4 k4 l4 m4 a5 b5 l5 m5 a6 b6 l6 m6
a7 b7 c7 m7 a8 b8 c8 m8 a9 b9 c9 d9
)
)
Я не сторонник того, чтобы детали модели смешивались с вопросами визуализации, но до тех пор, пока не требуется отделить одно от другого (например отобразить доску в «честном» 3D, а не изометрии) такой подход вполне работает. Рассмотрим это описание подробнее:
- Неотъемлемой частью описания является файл, содержащий изображение доски. Все геометрические размеры и позиции фигур привязаны к нему (именно по этой причине, большую часть дистрибутива моей реализации "Сокобана" составляют чёрные прямоугольники различных форм и размеров). Файл содержащий изображение доски в BMP-формате (ZoG понимает только этот формат) определяется ключевым словом image. Здесь можно определить сразу несколько файлов (для обеспечения возможности переключения между скинами), но лишь с идентичными геометрическими пропорциями.
- Ключевое слово grid позволяет описать n-мерный массив позиций. В большинстве случаев, это привычная двумерная доска, но также можно определять и доски другой размерности (вплоть до пяти). Доска может состоять из нескольких grid-ов, при условии того, что обеспечивается уникальное именование отдельных позиций. При большом желании, можно даже размещать один grid поверх другого, наподобие того как это сделано в "Квантовых крестиках-ноликах".
- Размер «ячейки» и расположение сетки определяются ключевым словом start-rectangle. Две пары целых чисел задают экранные координаты (x, y) левого верхнего и правого нижнего угла самой первой (левой верхней) ячейки.
- Далее следует описание «измерений» (dimensions). Каждое описание содержит строку имён (из которых декартовым произведением комбинируются имена позиций), а также два целых числа. В этих числах и заключается «магия», позволяющая описывать гексагональные и изометрические доски. Это ни что иное как сдвиги, на которые смещаются очередные ячейки сетки. Обычно (для двумерных досок), в одном из измерений, ячейки смещаются на ширину ячейки по x, а в другом — на высоту ячейки по y, но дополнительно смещая эти ячейки на половину ширины по x, можно получить превосходную основу для гексагональной доски.
- Вторая составляющая «магии» grid-ов — направления (directions). Доска — это не только позиции, но и связи (именованные и однонаправленные) между ними. Конечно, никто не мешает определить каждую связь индивидуально, задав имя и пару позиций для каждого соединения, но при определении досок больших размеров, этот процесс не будет весел. Ключевое слово directions позволяет манипулировать не именами позиций, а направлениями внутри сетки.
- Чтобы получить доску требуемой формы, мы берём «прямоугольную» доску большего размера, а затем смещаем ряды на половину ячейки друг относительно друга. В результате остаются «лишние» позиции, которые необходимо «отрезать» от доски. Ключевое слово kill-positions позволяет объявить ранее определённое имя позиции недействительным. Разумеется, вместе с удаляемыми позициями разрываются и соответствующие им соединения.
Использование ключевого слова grid позволяет существенно снизить объём ручной работы при описании «типовых» досок, но такой подход не лишён определённых недостатков. Во первых, если изображение доски не рисовалось под выбранные геометрические размеры специально, оперируя лишь целочисленными координатами и смещениями, бывает сложно выровнять расположение всех позиций доски идеально. Индивидуальное описание позиций менее лаконично, но позволяет корректировать их расположение независимо друг от друга. Вместе с тем, оно требует просто убийственного объёма ручной работы (с учётом необходимости исправления всех допущенных опечаток). Чтобы как-то облегчить этот процесс, я использую grid для «чернового» описания, после чего получаю индивидуальное описание позиций, при помощи небольшого скрипта:
my @grid;
my %kp;
my $sx, $sy, $dx, $dy;
my $dm = 0;
while (<>) {
if (/(start-rectangles+(d+)s+(d+)s+(d+)s+(d+))/) {
$sx = $1;
$sy = $2;
$dx = $3 - $1;
$dy = $4 - $2;
}
if (/("([^"]+)"s+((-?d+)s+(-?d+)))/) {
my @a = split(///, $1);
$grid[$dm]->{ix} = @a;
$grid[$dm]->{x} = $2;
$grid[$dm]->{y} = $3;
$dm++;
}
if (/(kill-positions/) {
$fl = 1;
}
if ($fl) {
if (/s(([a-z0-9]{1,2}s+)+)/i) {
my @a = split(/s+/, $1);
foreach my $p (@a) {
$kp{$p} = 1;
}
}
if (/)/) {
$fl = 0;
}
}
}
sub try {
my ($ix, $pos, $x, $y) = @_;
if ($ix < $dm) {
my $i = 0;
foreach my $p (@{$grid[$ix]->{ix}}) {
try($ix + 1, $pos . $p, $x + $i * $grid[$ix]->{x}, $y + $i * $grid[$ix]->{y});
$i++;
}
} else {
if (!$kp{$pos}) {
my $a = $sx + $x;
my $b = $sy + $y;
my $c = $a + $dx;
my $d = $b + $dy;
print " ";
printf "($pos %3d %3d %3d %3d)n", $a, $b, $c, $d;
}
}
}
try(0, '', 0, 0);
(positions
(a1 48 32 108 82)
(a2 18 84 78 134)
(b1 108 32 168 82)
(b2 78 84 138 134)
(b3 48 136 108 186)
(b4 18 188 78 238)
(c1 168 32 228 82)
(c2 138 84 198 134)
(c3 108 136 168 186)
(c4 78 188 138 238)
(c5 48 240 108 290)
(c6 18 292 78 342)
(d1 228 32 288 82)
(d2 198 84 258 134)
(d3 168 136 228 186)
(d4 138 188 198 238)
(d5 108 240 168 290)
(d6 78 292 138 342)
(d7 48 344 108 394)
(d8 18 396 78 446)
(e1 288 32 348 82)
(e2 258 84 318 134)
(e3 228 136 288 186)
(e4 198 188 258 238)
(e5 168 240 228 290)
(e6 138 292 198 342)
(e7 108 344 168 394)
(e8 78 396 138 446)
(e9 48 448 108 498)
(f1 348 32 408 82)
(f2 318 84 378 134)
(f3 288 136 348 186)
(f4 258 188 318 238)
(f5 228 240 288 290)
(f6 198 292 258 342)
(f7 168 344 228 394)
(f8 138 396 198 446)
(f9 108 448 168 498)
(g1 408 32 468 82)
(g2 378 84 438 134)
(g3 348 136 408 186)
(g4 318 188 378 238)
(g5 288 240 348 290)
(g6 258 292 318 342)
(g7 228 344 288 394)
(g8 198 396 258 446)
(g9 168 448 228 498)
(h1 468 32 528 82)
(h2 438 84 498 134)
(h3 408 136 468 186)
(h4 378 188 438 238)
(h5 348 240 408 290)
(h6 318 292 378 342)
(h7 288 344 348 394)
(h8 258 396 318 446)
(h9 228 448 288 498)
(i1 528 32 588 82)
(i2 498 84 558 134)
(i3 468 136 528 186)
(i4 438 188 498 238)
(i5 408 240 468 290)
(i6 378 292 438 342)
(i7 348 344 408 394)
(i8 318 396 378 446)
(i9 288 448 348 498)
(j3 528 136 588 186)
(j4 498 188 558 238)
(j5 468 240 528 290)
(j6 438 292 498 342)
(j7 408 344 468 394)
(j8 378 396 438 446)
(j9 348 448 408 498)
(k5 528 240 588 290)
(k6 498 292 558 342)
(k7 468 344 528 394)
(k8 438 396 498 446)
(k9 408 448 468 498)
(l7 528 344 588 394)
(l8 498 396 558 446)
(l9 468 448 528 498)
(m9 528 448 588 498)
)
Это лишь половина дела! Имена позиций доски необходимо поправить, чтобы привести их в соответствие с общепринятой нотацией. Кроме того, требуется связать пары позиций направлениями, не забыв «зациклить» доску по краям. Всё вместе вылилось в немаленький объём ручной работы, но я не стал писать под это дело скрипт (хотя возможно и стоило).
Сон разума
Хоть я и познакомился с «Чейзом» довольно давно, поиграть в него, до последнего времени, никак не удавалось. Очень уж причудливая для этого требуется доска. При некоторой сноровке, можно играть на доске Сёги (9x9), но её у меня тоже не было. Обычная шахматная доска (8x8) для этой игры непригодна совершенно. Доску для «Чейза» удалось приобрести на прошлом "Зилантконе", но кубики в комплект не входили. Своё приобретение я забросил на дальнюю полку и там бы оно вероятно и провалялось, если бы в дело не вмешался случай.
Тут-то я и вспомнил про «Чейз». Предстояло пополнить его комплект двадцатью игральными кубиками, но поскольку я всё равно направлялся в магазин настольных игр (за подарком), это (как мне тогда казалось) не являлось проблемой. На сайте, я присмотрел себе замечательные полупрозрачные кубики (по 70 рублей за штуку), но жизнь внесла коррективы. В магазине выяснилось, что присмотренные мной кубики имеются лишь в одном экземпляре. Что я могу сказать, Казань — не Москва, пришлось удовольствоваться бюджетным вариантом и набирать вожделенные кубики из предложенной продавцом россыпи ико-, доде- и прочих -аэдров. Красный или зелёный комплект собрать не удалось, но синие и белые (ладно, ладно, один слегка желтоватый) кубики в наличии имелись.
Правила я, разумеется, переврал (рассказывал о памяти). В моём изложении, траектории разлёта «осколков», на выходе из «репликатора», напоминали не наконечник стрелы, а скорее латинскую букву 'Y'. По всей видимости, определённую роль сыграло её сходство со схемами распада элементарных частиц. «Осколки» двигались не на одну клетку (как в оригинальном варианте правил), а в соответствии с их «номиналом». Кроме того, такой ход было гораздо легче заблокировать. Любые препятствия (будь то фигура, стоящая на пути разлёта «осколков» или наличие на доске десяти фигур) трактовались как невозможность выполнения хода. В оригинальной версии правил, заблокировать "Chamber" можно лишь установив фигуру на пути входа в него.
Другим звеном "испорченного телефона" послужил сам Дмитрий. В своём описании «Чейза» он упомянул, что фигура, выполнившая взятие, имеет право на повторный ход (по аналогии с Шашками). В первоисточнике не было ни слова об этом (о чём ему не преминул сообщить уважаемый Гест), но я, в тот момент, не обратил на это внимания. Надо сказать, идея скрестить «Чейз» с «Шашками» уже тогда вызывала много вопросов. Следовало ли распространять правило повторного хода на случай bumping-а? На «осколки», полученные при разделении фигуры? Что следовало делать если взятие выполнял каждый из осколков? А если то же с bumping-ом? Но, нет таких сложностей, которых мы не могли бы себе создать! Я с энтузиазмом принялся за работу…
Я не в восторге от реализации составных ходов в ZoG и вот почему. Прежде всего, в понимании ZoG частичные ходы — это именно отдельные, независимые действия. По сути, это просто набор ходов, выполняемых одним и тем же игроком, друг за другом. Мы не можем передавать какую либо промежуточную информацию между частичными ходами! Глобальные и позиционные флаги автоматически сбрасываются, в начале каждого хода. Это дьявольски неудобно, но это лишь часть беды! ZoG не может рассматривать составной ход как единую сущность (в частности, именно по этой причине пришлось вводить хардкодную опцию "maximal captures", для реализации «правила большинства». Какие-то другие идеи, не укладывающиеся в этот хардкод, реализовать уже не удастся!
Это фрагмент партии из игры "Mana", придуманной Клодом Лероем. Количество чёрточек, на каждой позиции, показывает, на сколько шагов может переместиться фигура. Должно быть выполнено точное число шагов и, при этом, в процессе движения нельзя поворачиваться назад. Тут-то нас и поджидает засада! Очень редко, но бывает так, что фигура, выполнив два шага, загоняет себя «в тупик». Она не может продолжить движение, поскольку ей мешают другие фигуры и обязана сделать ещё один шаг, поскольку должна завершить ход! А ZoG, в свою очередь, не предоставляет ровно никаких средств, чтобы решить эту проблему!
Другим ограничением является то, что составной ход может продолжать лишь та же самая фигура, которая перемещалась предыдущим частичным ходом. Именно так всё и происходит в шашках, но в «Чейзе» ситуация немного сложнее. Например, взятие может быть осуществлено при помощи bumping-а, то есть не той фигурой, которая выполняла ход! С Chamber-ходом всё ещё сложнее. Оба осколка могут взять фигуры противника и, по логике, имеют право выполнить следующий частичный ход. И обе они не являются той фигурой которая заходила в Chamber (той фигуры, на доске, вообще уже нет)!
: val ( -- n )
piece-type mark -
;
: mirror ( 'dir -- 'dir )
DUP ['] nw = IF
DROP ['] sw
ELSE
DUP ['] ne = IF
DROP ['] se
ELSE
DUP ['] sw = IF
DROP ['] nw
ELSE
['] se = verify
['] ne
ENDIF
ENDIF
ENDIF
;
: step ( 'dir -- 'dir )
DUP EXECUTE NOT IF
mirror
DUP EXECUTE verify
ENDIF
;
: bump ( 'dir -- )
BEGIN
here E5 <> verify
friend? here from <> AND IF
piece-type SWAP step SWAP
create-piece-type
FALSE
ELSE
TRUE
ENDIF
UNTIL DROP
;
: slide ( 'dir n -- )
alloc-path !
val SWAP BEGIN
step
SWAP 1- DUP 0= IF
TRUE
ELSE
my-empty? verify
SWAP FALSE
ENDIF
UNTIL DROP
from here move
+ enemy? IF
+ cont-type partial-move-type
+ ENDIF
bump enemy? IF
alloc-all
ELSE
alloc-path @ 0= verify
ENDIF
add-move
;
В конечном счёте, всё сводится к добавлению вызова partial-move-type при взятии вражеской фигуры (до выполнения bumping-а). Ограничения, о которых я говорил выше, остаются в силе. Мы не можем выполнить частичный ход, если взятие было осуществлено не той фигурой которая начала ход (в результате bumping-а или «расщепления» в Chamber), но даже в таком виде, этот код был бы неплохим решением. Если бы он заработал:

Я так и не смог расшифровать этот ребус и просто отослал код разработчику Axiom. Грег пока не ответил, но вроде бы работает над выпуском патча, который, я надеюсь, решит проблему. Странно здесь то, что частичные ходы в Axiom действительно работают! Более того, они существенно расширяют функциональность ZRF. Всё это хорошо описано в документации и используется в нескольких приложениях. Видимо, мне просто не повезло.
Поскольку частичные ходы не работали, пришлось искать другой способ решения проблемы. Если не удаётся выполнить все действия в рамках одного хода, можно попробовать растянуть их на несколько ходов! Я уже делал так в других играх, создавая на доске специальную невидимую позицию, на которой размещалась фигура-флаг. Если фигура принадлежала противнику, игрок знал, что должен пропустить свой ход. Это небольшое изменение, но оно потянуло за собой другие. Мне пришлось помечать фигуры, продолжающие ход (теперь это могли быть не только фигуры, начавшие ход), а также усложнить порядок передачи хода. В целом, это было довольно громоздкое и очень неуклюжее решение.
Результатом моих усилий стала весьма оригинальная модификация игры, к сожалению имевшая слишком мало общего с оригиналом. Кроме того, использование «сложного» порядка передачи ходов (turn-order) наотмашь било по «интеллекту» AI. Используемый им минимаксный алгоритм крайне негативно реагирует на подобные вольности, а в «иммунном» к ним search-engine (альтернативном варианте построения Axiom AI) невероятно сложно реализовать поиск в глубину.
По хлебным крошкам
Хорошо, допустим мы, своим ходом, забираем одну (или даже две фигуры) противника, после чего, распределяем полученные очки по оставшимся его фигурам, обязательно начиная с младших. Но как быть, если младших фигур несколько? Например, в самом начале игры, у каждого из игроков имеется по две «единички». Взяв любую фигуру номиналом от одного до пяти очков, мы получим два варианта распределения очков и ход игры может серьёзным образом измениться, в зависимости от того, какой из них мы выберем.
- Каждая фигура может иметь номинал от 1 до 6 очков
- Количество фигур не может превышать 10
- Суммарное количество очков всегда равно 25
Не сомневаюсь, что у этой задачи есть красивое аналитическое решение (возможно читатели мне его подскажут), но я не стал его искать. Я просто составил скрипт для генерации всех возможных наборов фигур, удовлетворяющих заданным условиям. Фигуры в наборах упорядочены по номиналу, поскольку именно в этом порядке распределяются взятые очки.
my @d;
my %s;
sub out {
my ($deep) = @_;
for (my $i = 0; $i < $deep; $i++) {
print "$d[$i]";
}
print "n";
}
sub dice {
my ($start, $deep, $sum) = @_;
if ($sum == 25) {
out($deep);
}
if ($deep < 10 && $sum < 25) {
for (my $i = $start; $i <= 6; $i++) {
$d[$deep] = $i;
dice($i, $deep + 1, $sum + $i);
}
}
}
dice(1);
1111111666
1111112566
1111113466
1111113556
1111114456
1111114555
1111122466
1111122556
1111123366
1111123456
1111123555
1111124446
1111124455
111112666
1111133356
1111133446
1111133455
1111134445
111113566
1111144444
111114466
111114556
111115555
1111222366
1111222456
1111222555
1111223356
1111223446
1111223455
1111224445
111122566
1111233346
1111233355
1111233445
1111234444
111123466
111123556
111124456
111124555
1111333336
1111333345
1111333444
111133366
111133456
111133555
111134446
111134455
11113666
111144445
11114566
11115556
1112222266
1112222356
1112222446
1112222455
1112223346
1112223355
1112223445
1112224444
111222466
111222556
1112233336
1112233345
1112233444
111223366
111223456
111223555
111224446
111224455
11122666
1112333335
1112333344
111233356
111233446
111233455
111234445
11123566
111244444
11124466
11124556
11125555
1113333334
111333346
111333355
111333445
111334444
11133466
11133556
11134456
11134555
11144446
11144455
1114666
1115566
1122222256
1122222346
1122222355
1122222445
1122223336
1122223345
1122223444
112222366
112222456
112222555
1122233335
1122233344
112223356
112223446
112223455
112224445
11222566
1122333334
112233346
112233355
112233445
112234444
11223466
11223556
11224456
11224555
1123333333
112333336
112333345
112333444
11233366
11233456
11233555
11234446
11234455
1123666
11244445
1124566
1125556
113333335
113333344
11333356
11333446
11333455
11334445
1133566
11344444
1134466
1134556
1135555
1144456
1144555
115666
1222222246
1222222255
1222222336
1222222345
1222222444
122222266
1222223335
1222223344
122222356
122222446
122222455
1222233334
122223346
122223355
122223445
122224444
12222466
12222556
1222333333
122233336
122233345
122233444
12223366
12223456
12223555
12224446
12224455
1222666
122333335
122333344
12233356
12233446
12233455
12234445
1223566
12244444
1224466
1224556
1225555
123333334
12333346
12333355
12333445
12334444
1233466
1233556
1234456
1234555
1244446
1244455
124666
125566
133333333
13333336
13333345
13333444
1333366
1333456
1333555
1334446
1334455
133666
1344445
134566
135556
1444444
144466
144556
145555
16666
2222222236
2222222245
2222222335
2222222344
222222256
2222223334
222222346
222222355
222222445
2222233333
222223336
222223345
222223444
22222366
22222456
22222555
222233335
222233344
22223356
22223446
22223455
22224445
2222566
222333334
22233346
22233355
22233445
22234444
2223466
2223556
2224456
2224555
223333333
22333336
22333345
22333444
2233366
2233456
2233555
2234446
2234455
223666
2244445
224566
225556
23333335
23333344
2333356
2333446
2333455
2334445
233566
2344444
234466
234556
235555
244456
244555
25666
33333334
3333346
3333355
3333445
3334444
333466
333556
334456
334555
344446
344455
34666
35566
444445
44566
45556
55555
Всего 294 возможных варианта. Впрочем, это только половина дела. Нам более интересны не сами расклады, а то, какими способами мы сможем разместить очки взятой фигуры в каждом из них. Не буду утомлять читателя подробными рассуждениями, покажу лишь скрипт и окончательный результат его работы:
my @d;
my %s;
sub out {
my ($deep) = @_;
for (my $i = 0; $i < $deep; $i++) {
print "$d[$i]";
}
print "n";
}
sub proc {
my ($x, $r, $m) = @_;
if ($x == 0) {
$s{$r}++;
} else {
my $n = $x % 10;
for (my $i = 0; $i < $n; $i++) {
proc(int($x / 10), $r + $i * $m, $m * 10);
}
}
}
sub alloc {
my ($x, $deep, $res) = @_;
if ($x == 0) {
proc($res, 0, 1);
} else {
my $vl = 6;
for (my $i = 0; $i < $deep; $i++) {
if ($d[$i] < $vl) {
$vl = $d[$i];
}
}
if ($vl < 6) {
my $cn = 0;
my $ix = 0;
for (my $i = 0; $i < $deep; $i++) {
if ($d[$i] == $vl) {
$cn++;
$ix = $i;
}
}
my $y = $d[$ix]; $d[$ix] = 6;
$x -= 6 - $vl;
if ($x < 0) {
$x = 0;
}
alloc($x, $deep, $res * 10 + $cn);
$d[$ix] = $y;
}
}
}
sub dice {
my ($start, $deep, $sum) = @_;
if ($sum == 25) {
for (my $i = 0; $i < $deep; $i++) {
my $x = $d[$i]; $d[$i] = 6;
alloc($x, $deep, 0);
$d[$i] = $x;
}
}
if ($deep < 10 && $sum < 25) {
for (my $i = $start; $i <= 6; $i++) {
$d[$deep] = $i;
dice($i, $deep + 1, $sum + $i);
}
}
}
dice(1, 0, 0);
my $all;
foreach my $k (sort { $s{$a} <=> $s{$b} } keys %s) {
$all += $s{$k};
print "$kt=> $s{$k}n";
}
print "n$alln";102 => 1
331 => 1
200 => 1
...
22 => 93
5 => 106
21 => 152
20 => 152
11 => 152
10 => 220
4 => 259
3 => 584
2 => 1061
1 => 1677
0 => 2407
7954
Слева — цепочки цифр, управляющие порядком распределения взятых очков. Например, «20» означает, что мы начинаем распределение с первой попавшейся фигуры (мы начинаем их подсчёт с 0), затем, распределяем в третью из оставшихся фигур с минимальным номиналом. Очевидно, что такая схема распределения возможна лишь для раскладов, не менее чем с четырьмя «минимальными» фигурами, например «3333445» (причём, распределить таким образом получится только «четвёрку» или «пятёрку»). Результат работы скрипта показывает, что распределяя очки, каждый раз в первую попавшуюся «минимальную» фигуру, мы покроем 30% (2407/7954) всех возможных ситуаций, а используя всего лишь три схемы распределения, уже более 64%!
Специально для таких случаев, ZoG предоставляет интересную интерфейсную возможность. Выполняя ход, игрок указывает два поля: начальное и конечное. В том случае, если существует несколько различных возможных ходов, соединяющих выбранную пару полей, игроку предоставляется возможность выбора (всплывающее меню). Простейший пример — превращение пешек в Шахматах. Дойдя до последней горизонтали, пешка может превратиться в любую из фигур (от слона до ферзя) и выбор должен быть сделан игроком. Именно этой опцией я и решил воспользоваться.
VARIABLE alloc-path
VARIABLE alloc-val
VARIABLE alloc-target
VARIABLE alloc-pos
: alloc-to ( pos -- )
DUP add-pos
DUP val-at 6 SWAP -
DUP alloc-val @ > IF
DROP alloc-val @
0 alloc-val !
ELSE
alloc-val @ OVER - alloc-val !
ENDIF
my-next-player ROT ROT
OVER piece-type-at + SWAP
create-player-piece-type-at
;
: alloc ( -- )
6 0 BEGIN
DUP enemy-at? OVER not-in-pos? AND IF
SWAP OVER val-at MIN SWAP
ENDIF
1+ DUP A9 >
UNTIL DROP
DUP 6 < IF
alloc-target !
alloc-path @ 10 MOD alloc-pos !
0 BEGIN
DUP enemy-at? OVER not-in-pos? AND IF
DUP val-at alloc-target @ = IF
alloc-pos @ 0= IF
DUP alloc-to
0 alloc-target !
DROP A9
ELSE
alloc-pos --
ENDIF
ENDIF
ENDIF
1+ DUP A9 >
UNTIL DROP
alloc-target @ 0= verify
alloc-val @ 0> IF
alloc-path @ 10 / alloc-path !
RECURSE
ENDIF
ELSE
DROP
ENDIF
;
: alloc-all ( -- )
0 pos-count !
here add-pos
alloc
;
Переменная alloc-path содержит нашу последовательность «хлебных крошек». Разумеется, было бы совершенно слишком расточительно определять в коде все 105 возможных управляющих последовательностей, но мы уже выяснили, что они не равнозначны. Большинство из них будут использоваться крайне редко, а всего 4 из них покроют большую часть возможных случаев. К сожалению, даже этим воспользоваться не удалось:
: eat ( 'dir n -- )
LITE-VERSION NOT IF
check-pass
check-neg
ENDIF
+ alloc-path !
val SWAP BEGIN
step
SWAP 1- DUP 0= IF
TRUE
ELSE
my-empty? verify
SWAP FALSE
ENDIF
UNTIL DROP
from here move
LITE-VERSION NOT enemy? AND IF
from piece-type-at mark - ABS
mark SWAP - create-piece-type
ENDIF
bump DROP
here E5 <> verify
enemy? verify
LITE-VERSION NOT IF
clear-neg
set-pass
ENDIF
+ val alloc-val !
+ alloc-all
add-move
;
: eat-nw-0 ( -- ) ['] nw 0 eat ;
: eat-sw-0 ( -- ) ['] sw 0 eat ;
: eat-ne-0 ( -- ) ['] ne 0 eat ;
: eat-se-0 ( -- ) ['] se 0 eat ;
: eat-w-0 ( -- ) ['] w 0 eat ;
: eat-e-0 ( -- ) ['] e 0 eat ;
: eat-nw-1 ( -- ) ['] nw 1 eat ;
: eat-sw-1 ( -- ) ['] sw 1 eat ;
: eat-ne-1 ( -- ) ['] ne 1 eat ;
: eat-se-1 ( -- ) ['] se 1 eat ;
: eat-w-1 ( -- ) ['] w 1 eat ;
: eat-e-1 ( -- ) ['] e 1 eat ;
: eat-nw-2 ( -- ) ['] nw 2 eat ;
: eat-sw-2 ( -- ) ['] sw 2 eat ;
: eat-ne-2 ( -- ) ['] ne 2 eat ;
: eat-se-2 ( -- ) ['] se 2 eat ;
: eat-w-2 ( -- ) ['] w 2 eat ;
: eat-e-2 ( -- ) ['] e 2 eat ;
: eat-nw-3 ( -- ) ['] nw 3 eat ;
: eat-sw-3 ( -- ) ['] sw 3 eat ;
: eat-ne-3 ( -- ) ['] ne 3 eat ;
: eat-se-3 ( -- ) ['] se 3 eat ;
: eat-w-3 ( -- ) ['] w 3 eat ;
: eat-e-3 ( -- ) ['] e 3 eat ;
{moves p-moves
{move} split-nw-0 {move-type} normal-priority
{move} split-ne-0 {move-type} normal-priority
{move} split-sw-0 {move-type} normal-priority
{move} split-se-0 {move-type} normal-priority
{move} split-w-0 {move-type} normal-priority
{move} split-e-0 {move-type} normal-priority
{move} split-nw-1 {move-type} normal-priority
{move} split-ne-1 {move-type} normal-priority
{move} split-sw-1 {move-type} normal-priority
{move} split-se-1 {move-type} normal-priority
{move} split-w-1 {move-type} normal-priority
{move} split-e-1 {move-type} normal-priority
+ {move} eat-nw-0 {move-type} normal-priority
+ {move} eat-ne-0 {move-type} normal-priority
+ {move} eat-sw-0 {move-type} normal-priority
+ {move} eat-se-0 {move-type} normal-priority
+ {move} eat-w-0 {move-type} normal-priority
+ {move} eat-e-0 {move-type} normal-priority
+ {move} eat-nw-1 {move-type} normal-priority
+ {move} eat-ne-1 {move-type} normal-priority
+ {move} eat-sw-1 {move-type} normal-priority
+ {move} eat-se-1 {move-type} normal-priority
+ {move} eat-w-1 {move-type} normal-priority
+ {move} eat-e-1 {move-type} normal-priority
+ {move} eat-nw-2 {move-type} normal-priority
+ {move} eat-ne-2 {move-type} normal-priority
+ {move} eat-sw-2 {move-type} normal-priority
+ {move} eat-se-2 {move-type} normal-priority
+ {move} eat-w-2 {move-type} normal-priority
+ {move} eat-e-2 {move-type} normal-priority
+ {move} eat-nw-3 {move-type} normal-priority
+ {move} eat-ne-3 {move-type} normal-priority
+ {move} eat-sw-3 {move-type} normal-priority
+ {move} eat-se-3 {move-type} normal-priority
+ {move} eat-w-3 {move-type} normal-priority
+ {move} eat-e-3 {move-type} normal-priority
{move} slide-nw {move-type} normal-priority
{move} slide-ne {move-type} normal-priority
{move} slide-sw {move-type} normal-priority
{move} slide-se {move-type} normal-priority
{move} slide-w {move-type} normal-priority
{move} slide-e {move-type} normal-priority
-( {move} exchange-1-nw {move-type} normal-priority
- {move} exchange-1-ne {move-type} normal-priority
- {move} exchange-1-sw {move-type} normal-priority
- {move} exchange-1-se {move-type} normal-priority
- {move} exchange-1-w {move-type} normal-priority
- {move} exchange-1-e {move-type} normal-priority
- {move} exchange-2-nw {move-type} normal-priority
- {move} exchange-2-ne {move-type} normal-priority
- {move} exchange-2-sw {move-type} normal-priority
- {move} exchange-2-se {move-type} normal-priority
- {move} exchange-2-w {move-type} normal-priority
- {move} exchange-2-e {move-type} normal-priority
- {move} exchange-3-nw {move-type} normal-priority
- {move} exchange-3-ne {move-type} normal-priority
- {move} exchange-3-sw {move-type} normal-priority
- {move} exchange-3-se {move-type} normal-priority
- {move} exchange-3-w {move-type} normal-priority
- {move} exchange-3-e {move-type} normal-priority
- {move} exchange-4-nw {move-type} normal-priority
- {move} exchange-4-ne {move-type} normal-priority
- {move} exchange-4-sw {move-type} normal-priority
- {move} exchange-4-se {move-type} normal-priority
- {move} exchange-4-w {move-type} normal-priority
- {move} exchange-4-e {move-type} normal-priority
- {move} exchange-5-nw {move-type} normal-priority
- {move} exchange-5-ne {move-type} normal-priority
- {move} exchange-5-sw {move-type} normal-priority
- {move} exchange-5-se {move-type} normal-priority
- {move} exchange-5-w {move-type} normal-priority
- {move} exchange-5-e {move-type} normal-priority )
moves}
По всей видимости, в Axiom имеется ограничение на количество определяемых ходов (никак не отражённое в документации). Как я это определил? Очень просто! Когда я добавляю в код все определения, программа крэшится при старте. Если я убираю часть определений (например exchange-ходы), всё работает нормально. К сожалению, от идеи вариативного распределения очков пришлось отказаться.
Строго говоря, это не вполне корректное решение. По правилам «Чейза», распределять очки должен не тот игрок, который выполнил ход, а его противник. Я не имею ни малейшего представления, о том, как этого можно добиться, используя ZoG, но есть очень простой обходной путь. Интерфейс ZoG предоставляет удобную интерфейсную возможность редактирования доски. Используя команды всплывающего меню, игрок может удалить любую фигуру на доске или создать другую. Эта возможность незаменима при отладке и я часто ей пользуюсь. В общем, игрок которому не понравилось автоматическое распределение очков, может легко перераспределить их вручную (очерёдность хода, при этом, не нарушается). Необходимо соблюдать лишь минимальную осторожность. В процессе редактирования не следует допускать ситуации, когда у одного из игроков остаётся менее 5 фигур, поскольку в этом случае, ему будет немедленно засчитано поражение и игра будет остановлена.
… считай до одного!
Поскольку идея «вариативного» распределения съеденных очков провалилась, я вернулся к разработке игры, посредством ZRF. Axiom-реализация, в принципе, тоже работала, но ей всё ещё не хватало AI (штатным ZoG-овским Аксиома пользоваться не умеет). В целом, эта задача сводится к правильному кодированию оценочной функции (для эстетов есть ещё и "Custom Engine"), но и это — весьма не просто! Во всяком случае, стандартная оценочная функция, учитывающая мобильность и материальный баланс, в «Чейзе» проявила себя не лучшим образом.
: OnEvaluate ( -- score )
mobility
current-player material-balance KOEFF * +
;
Самый хитрый зверь здесь — mobility. Фактически — это количество всех возможных ходов игрока, из которого вычитается количество всех возможных ходов противника. Все ходы игрока, на момент оценки позиции, уже сгенерированы — подсчитать их не сложно, а вот чтобы сгенерировать ходы противника, приходится использовать немножко аксиомовской магии:
: mobility ( -- score )
move-count
current-player TRUE 0 $GenerateMoves
move-count -
$DeallocateMoves
;
Далее, полученная «мобильность» складывается с «материальным балансом», умноженным на некоторый константный коэффициент. Материальный баланс — это просто суммарная стоимость всех своих фигур, за вычетом стоимости фигур противника. Кстати, это объясняет, почему для фигур в Axiom я выбрал такие странные числовые значения:
{pieces
{piece} p1 {moves} p-moves 6 {value}
{piece} p2 {moves} p-moves 5 {value}
{piece} p3 {moves} p-moves 4 {value}
{piece} p4 {moves} p-moves 3 {value}
{piece} p5 {moves} p-moves 2 {value}
{piece} p6 {moves} p-moves 1 {value}
pieces}
Я стремился сделать «мелкие» фигуры более значимыми, поскольку игроку действительно выгодно держать на доске как можно больше мелких фигур. В общем, в таком виде, всё это не сработало! AI вёл себя просто ужасно. Иногда складывалось впечатление, что он целенаправленно стремиться проиграть. Я думал о том как улучшить оценочную функцию, включив в неё бонусы/штрафы за взаимные угрозы фигур, образование кластеров (из фигур, стоящих вплотную друг к другу), достижимости Chamber и пр., но решил не тратить на это время, а просто переключиться на ZRF. Штатный AI ZoG-а традиционно показывает себя сильным, в подобных играх.
Оставалась всего одна мелочь — в ZRF напрочь отсутствовала арифметика! «Чейз» — такая игра, в которой постоянно приходится считать! В некоторых случаях можно выкрутится. Например, при определении поражения игрока, вместо подсчёта очков (до 25-ти) на всех фигурах, можно ограничиться стандартной проверкой количества фигур. Поскольку 25 очков заведомо невозможно разместить на 4 фигурах, и всегда можно распределить по большему количеству фигур, следующих условий завершения игры вполне достаточно:
(loss-condition (Red White) (pieces-remaining 4) )
(loss-condition (Red White) (pieces-remaining 3) )
Вторая проверка необходима, поскольку в игре возможна ситуация, когда одним ходом забираются сразу две фигуры (после расщепления фигуры в Chamber). К сожалению, есть одна задача, в которой целочисленная арифметика необходима! Разумеется, это распределение «съеденных» очков. В ZRF я не пытаюсь предложить несколько возможных вариантов распределения, на выбор. Мне необходимо просто обойти все фигуры, начиная с младших, и правильно добавить к ним ещё не распределённые очки. Вот как я это делаю:
(define clear
(set-flag $1-8 false) (set-flag $1-4 false)
(set-flag $1-2 false) (set-flag $1-1 false)
)
(define inc
(if (flag? $1-1)
(set-flag $1-1 false)
(if (flag? $1-2)
(set-flag $1-2 false)
(if (flag? $1-4)
(set-flag $1-4 false)
(if (flag? $1-8)
(set-flag $1-8 false)
else
(set-flag $1-8 true)
)
else
(set-flag $1-4 true)
)
else
(set-flag $1-2 true)
)
else
(set-flag $1-1 true)
)
)
(define dec
(if (not-flag? $1-1)
(set-flag $1-1 true)
(if (not-flag? $1-2)
(set-flag $1-2 true)
(if (not-flag? $1-4)
(set-flag $1-4 true)
(if (not-flag? $1-8)
(set-flag $1-8 true)
else
(set-flag $1-8 false)
)
else
(set-flag $1-4 false)
)
else
(set-flag $1-2 false)
)
else
(set-flag $1-1 false)
)
)
Пользоваться этим — совсем просто:
(define not-10?
(or (not-flag? $1-8)
(flag? $1-4)
(not-flag? $1-2)
(flag? $1-1)
)
)
(define calc
(clear x)
mark START
(while (on-board? next)
next
(if friend?
(inc x)
)
)
(verify (not-10? x))
back
)
Главный цирк, как и предполагалось, начинается когда дело доходит до распределения очков по фигурам. Для начала, эти очки необходимо получить из съедаемой фигуры. Здесь подход совершенно прямолинейный. ZRF — не знает чисел, но мы-то знаем!
(define init
(clear $1)
(if (or (piece? p1) (piece? p3) (piece? p5))
(set-flag $1-1 true)
)
(if (or (piece? p2) (piece? p3) (piece? p6))
(set-flag $1-2 true)
)
(if (or (piece? p4) (piece? p5) (piece? p6))
(set-flag $1-4 true)
)
)
Здесь, нас подстерегает маленькая засада. Если съедаемых фигур две (такое редко, но бывает), такой код совершенно не подходит, поскольку, в самом начале, обнуляет «число». Надо научиться складывать числа! Это просто:
(define sum
(while (not-0? $2)
(inc $1)
(dec $2)
)
)
Осталось немного, но главное. Как добавить часть «числа» к количеству очков на фигуре? Причём, не абы как, а начиная с младших фигур?
(define try-alloc
(if (is-0? x)
(inc y)
else
(dec x)
)
)
(define set-piece
(if (am-i-red?)
(create White $1)
else
(create Red $1)
)
)
(define alloc-to
(clear y)
(if (piece? p1)
(try-alloc) (try-alloc) (try-alloc) (try-alloc) (try-alloc)
)
(if (piece? p2)
(try-alloc) (try-alloc) (try-alloc) (try-alloc)
)
(if (piece? p3)
(try-alloc) (try-alloc) (try-alloc)
)
(if (piece? p4)
(try-alloc) (try-alloc)
)
(if (piece? p5)
(try-alloc)
)
(if (is-0? y)
(set-piece p6)
else
(if (is-1? y)
(set-piece p5)
else
(if (is-2? y)
(set-piece p4)
else
(if (is-3? y)
(set-piece p3)
else
(set-piece p2)
)
)
)
)
)
(define alloc
(if (not-0? x)
mark ST
(while (on-board? next)
next
(if (and enemy? (piece? $1) (not-0? x)
(not-position-flag? is-captured?))
(alloc-to)
)
)
back
)
)
(define alloc-all
(alloc p1) (alloc p2) (alloc p3) (alloc p4) (alloc p5)
)
При выполнении alloc-all, в x находится количество ещё не распределённых очков (максимум — 12, если съели две шестёрки). Пока в x не 0, пытаемся его распределить, начиная с p1 и до p5 (в шестёрки, очевидно, распределить уже ничего не удастся). Ищем фигуру требуемого номинала на доске и вызываем alloc-to. Здесь и начинается магия. Распределяем очки по одной единичке, в зависимости от типа фигуры (в p1 лезет 5 единичек. в p2 — 4 и т.д.). Не пытаемся анализировать, хватает ли в x единичек, а просто добавляем все распределяемые единички к ещё одной переменной — y. Это и есть переполнение (очевидно оно не может превышать 4), если оно не нулевое, просто корректируем тип фигуры.
В результате, вся наша «ненормальная арифметика» работает с вполне приемлемой производительностью и AI ничуть не страдает. Надо сказать, что не всегда подобные эксперименты бывают столь же удачны. Например, эту версию калькулятора (напомню, что никакой арифметики в ZRF нет) можно рассматривать исключительно как шутку. Его производительность просто ужасна! Но в нашем случае, «ненормальное программирование» показало себя лучшим из возможных решений.
Автор: GlukKazan
