Ранее habrahabr.ru/post/145309/ мы сделали обзор подхода к универсальному искусственному интеллекту (ИИ). Но что такое универсальный ИИ? Чего именно недостает современным практическим системам ИИ, чтобы называться универсальными? Для большей конкретности обсуждения этого вопроса давайте рассмотрим его на примере машинного обучения, являющегося необходимым компонентом ИИ.
Машинное обучение давно переросло границы области академического искусственного интеллекта и пришло к «обычным программистам». Во многих прикладных задачах используются практические методы data mining'а, распознавания образов, статистического вывода и т.д. Крупные фирмы устраивают разные курсы и школы по автоматическому анализу данных, создают базовые кафедры, участвуют в организации конференций и прочими способами несут в мир свет знания, накопленного в области машинного обучения. Ученые тоже не отстают: придумывают новые методы и прорабатывают новые подобласти, такие как модное ныне трансферное обучение.
Однако такое развитие этой области вширь не особо способствует ее развитию вглубь. Напротив, распространяются упрощенные истолкования основ машинного обучения (несмотря на то, что эти истолкования нередко подкреплены достаточно сложной теорией), позволяющие получать частные практические решения. Последнее, конечно, неплохо, но проблема универсальных методов машинного обучения остается нерешенной (и даже проигнорированной). При этом, с одной стороны, в среде «прикладников» популяризовались мифы об универсальных методах машинного обучения (типа нейронных сетей), которые в действительности таковыми не являются. С другой стороны, в среде «теоретиков» пропала вера в возможность создания универсальных методов машинного обучения, что выражается в том, что на любые попытки предложить какой-то новый универсальный метод априорно навешивается метка «Yet Another Classifier» или вспоминается «No Free Lunch» теорема.
Самым поразительным при этом является то, что теория действительно универсального машинного обучения существует уже пол века, и многие рассуждения современных исследователей в контексте этой теории выглядят весьма наивными. Что это за теория? Как она решает проблемы машинного обучения? Почему она не получила особого распространения до сих пор? И можно ли все же сделать универсальную систему машинного обучения? К ответам на эти вопросы мы постараемся приблизиться, но сначала покажем необходимость универсального обучения для сильного ИИ.
Основные проблемы машинного обучения можно продемонстрировать на примере такой «простой» задачи, как функциональная аппроксимация и экстраполяция. В конечном итоге интеллектуальному агенту нужно установить связь между сенсорным входом и моторным выходом или научиться экстраполировать величины подкреплений от среды в зависимости от совершенных действий, так что связь этой задачи с ИИ несомненна.
Посмотрим на последовательность точек, представленных на рис. 1. Как ее продолжить? По-началу кажется абсолютно естественным, что для решения этой задачи нужно подобрать функцию, которая проходит наиболее близко к имеющимся точкам, и эта функция будет наилучшим решением.
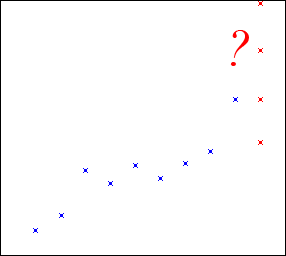
Рис. 1. Как продолжить точки?
В математике существуют различные теоремы о том, что некоторая произвольная функция, на вид которой не накладывается существенных ограничений (за исключением, разве что, непрерывности и дифференцируемости), может быть аппроксимирована функциями определенного вида с произвольной точностью. В частности, именно из-за таких теорем у искусственных нейронных сетей (ИНС) сложилась репутация универсальных аппроксиматоров. Забавно, что такая репутация сложилась именно у ИНС, а не, скажем, у многочленов, для которых сходные теоремы были доказаны гораздо раньше.
Но что эти теоремы значат с точки зрения машинного обучения? То, что приближение одних функций другими функциями в принципе возможно, вовсе не означает, что его можно выполнить на практике. Ведь на практике имеется обучающая выборка всегда конечного размера, да и к тому же нередко зашумленная. Посмотрим, как в таких условиях будет работать аппроксимация. Для этого используем многочлены, поскольку результат для них будет иметь более прозрачную интерпретацию.
Будем подбирать параметры многочленов разных степеней так, чтобы эти многочлены проходили наиболее близко к точкам обучающей выборки, то есть используем метод наименьших квадратов, который в данном случае имеет весьма простую реализацию. На рис. 2 показаны решения для линейной функции, параболы и кубической функции. Последняя (красная) точка не вошла в обучающую выборку и соответствует истинной зависимости.
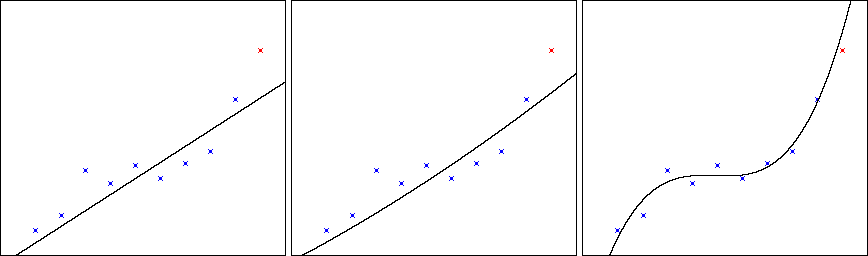
Рис. 2. Результаты построения многочленов 1-й, 2-й и 3-й степеней.
Как будто все хорошо: за счет увеличения степени многочлена удается как уменьшить отклонения от точек обучающей выборки, так и улучшить точность предсказания. Но попробуем продолжить увеличивать степень дальше. На рис. 3 показаны решения для многочленов 4-й, 7-й и 10-й степеней.
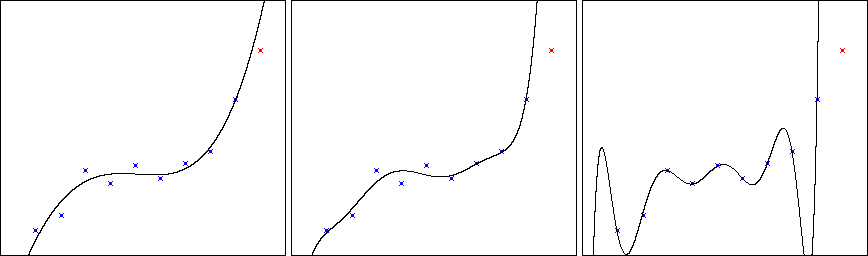
Рис. 3. Результаты построения многочленов 4-й, 7-й и 10-й степеней.
Как видно, точность на обучающей выборке увеличивается, и многочлен 10-й степени проходит идеально через все точки, но точность предсказания катастрофически падает! Это хорошо известный эффект чрезмерно близкой подгонки (overfitting). Кому-то этот эффект может показаться совершенно мистическим: «Мы же улучшаем аппроксимацию на имеющейся выборке, кроме которой никаких данных нет! Почему же она в действительности ухудшается?». А кому-то покажется банальным: «Чего же вы ожидали, если пытаетесь подогнать свою модель под шум в данных?». Однако независимо от отношения к этой проблеме, она никуда не исчезает. Проявляется она, естественно, и в случае ИНС. Эта проблема в области машинного обучения вездесуща: она характерна не только для аппроксимации и экстраполяции, но и для распознавания образов, сегментации, кластеризации и т.д. Как можно с ней справиться?
Здесь возможны разные подходы. В случае некоторых классов нейронных сетей обучение специально прерывают, пока ИНС не успела слишком сильно подстроиться под данные (при этом выработаны даже специальные эвристические критерии, определяющие наиболее подходящий момент для остановки обучения). В этой связи данный феномен имеет и второе название – переобучение (overlearning). Говоря по-простому, это зубрежка, при которой система концентрируется на конкретных примерах. Этот недостаток свойственен и обучению учащихся, если их обучение и оценка его качества производится по одним и тем же тестам.
Еще один незамысловатый способ борьбы с этим эффектом – это перекрестная проверка, или кроссвалидация, идея которой заключается в том, чтобы из обучающей выборки выделить контрольную. При этом обучение производится по одной части выборки, а качество обучения оценивается по другой части. То есть раз уж мы хотим, чтобы наше решение хорошо работало не на тех данных, на которых мы его обучали, а на новых данных, давайте так и будем проверять. У такого подхода есть свои недостатки. Во-первых, уменьшается размер обучающей выборки, а, значит, ухудшается и качество строящейся модели. Во-вторых, такой подход все равно склонен к переобучению, хотя и более слабому: чрезмерно близкая подгонка косвенно происходит по отношению к контрольной выборке (достаточно вспомнить, как школьников натаскивают на ЕГЭ без особой пользы для обучения). Чтобы ослабить и этот эффект, обучающую выборку делят на много частей (скажем, на 10) и попеременно качество решения тестируют на разных из них, что, однако, увеличивает время вычислений и усугубляет первый недостаток. И, в-третьих, данный подход не слишком легко применить при обучении без учителя.
В любом случае, ни раннее прерывание обучения, ни кроссвалидация не отвечают на вопрос о природе переобучения и выглядят странными: если плохо учиться долго или использовать при этом всю имеющуюся информацию, то что-то должно быть не так в самом процессе обучения. Попробуем разобраться. Переобучение возникает, когда пространство моделей слишком большое, например, используются полиномы произвольной степени или нейронные сети с любым числом нейронов (из-за этого иногда даже высказывается мысль, что на практике такие пространства рассматривать бессмысленно – в них слишком велика «свобода творчества», а это ныне не модно и при обучении людей). Значит, проблема заключается в том, чтобы из большого числа моделей выбрать наилучшую. Для ее решения нужен, по крайней мере, адекватный критерий качества моделей.
Некоторый намек на разгадку природы переобучения дает теория вероятностей. По правилу Байеса наилучшей моделью M данных D будет модель с максимальной апостериорной вероятностью P(M|D), которая пропорциональна произведению правдоподобия данных для этой модели P(D|M), умноженному на априорную вероятность модели P(M):
P(M|D) ~ P(D|M)P(M).
Здесь за точность, с которой модель описывает данные, отвечает правдоподобие, которое при предположении о нормальном распределении ошибок (отклонений модели от данных) явным образом выражается через среднеквадратичное отклонение. Если максимизировать только его (то есть пользоваться методом максимального правдоподобия), то как раз и возникает эффект переобучения. Значит, возможность в соответствии с правилом Байеса выбрать менее точную, но не склонную к переобучению, модель может быть обеспечена только априорными вероятностями P(M).
Проблема априорных вероятностей в статистическом выводе является фундаментальной. Ведь эти вероятности априорны, то есть должны быть каким-то чудом определены до получения данных. Если у нас есть много наборов данных, то априорные вероятности моделей – это вероятности того, что конкретная модель окажется лучшей для некоторого произвольного набора. Но это только усложняет задачу: ведь при определении априорных вероятностей по многим наборам данных нам опять потребуются какие-то априорные вероятности, чтобы не возникло переобучения. И так далее. Хоть мы и выяснили, что проблема переобучения связана с проблемой задания априорных вероятностей, но от этого пока не легче.
Интересное, однако, наблюдение можно сделать, если прологарифмировать правило Байеса и вместо максимизации самой апостериорной вероятности минимизировать минус логарифм от нее:
–log2P(M|D) ~ –log2P(D|M) – log2P(M).
Минус логарифм от вероятности – это просто количество информации, причем –log2P(M) – количество информации в модели (длина ее описания в битах), а –log2P(D|M) – дополнительное количество информации в данных, при уже имеющейся модели (по сути, длина описания отклонений данных от модели, характеризующая ее точность). Если отвлечься от способа вычисления количества информации через вероятности, то можно увидеть следующее. Количество информации в модели – это ее сложность. Скажем, чем больше членов у нашего многочлена или нейронов и связей между ними в ИНС, тем больше битов уйдет на кодирование таких моделей.
Необходимость поиска компромисса между сложностью модели и ее точностью выражается в принципе минимальной длины описания, который и гласит, что лучшей моделью является модель, для которой достигается минимум длины описания отклонений данных от модели (или данных, закодированных с помощью модели) и сложности самой модели. Этот принцип иногда называют формализацией правила бритвы Оккама, которое уже давно указывало, что не следует плодить сущностей сверх необходимости.
Здесь важно, что сложность модели можно считать непосредственно, а не через ее априорную вероятность. В действительности, существует корректная возможность ввести понятие количества информации до понятия вероятности (и теорию вероятностей выводить из теории информации, а не наоборот), и тем самым решить ряд фундаментальных проблем, свойственных как самой теории вероятностей, так и основанной на ней классической (Шенноновской) теории информации. Но это тема для отдельного разговора.
Итак, у модели должна быть тем меньше априорная вероятность, чем выше ее сложность. Такое штрафование моделей за сложность на практике неплохо заменяет другие методы устранения эффекта переобучения. Переобучение возникает при выборе слишком сложной модели. Чем модель проще, тем она является более общей. Очевидно, переобучение связано с недостаточным обобщением. Именно отсутствие обобщения и является причиной низкого качества обучения при зубрежке или подгонке обучения к тестам. Бывает, конечно, и другая крайность, когда с помощью одной простой модели пытаются описать слишком многое, невзирая на ошибки или на то, что модель не упрощает («не сжимает») данные. Информационный критерий позволяет найти правильный компромисс.
Однако общая проблема машинного обучения при этом все же не решается. Невозможность правильного обобщения может быть связана с тем, что нужной модели просто нет в используемом пространстве моделей.
Вернемся к примеру с полиномиальной аппроксимацией. Если истинной моделью у нас является многочлен, то все будет хорошо – критерий длины описания позволит выбрать многочлен с оптимальным числом параметров, обеспечивающий наилучшее (при имеющихся данных) предсказание. Но что произойдет, если данные порождены с помощью какой-то другой функции? Спасет ли нас то, что эта функция в принципе может быть приближена некоторым многочленом?
Возьмем, к примеру, экспоненту. Она описывается рядом слагаемых вида xn/n!. Но в этом ряде бесконечное число членов. А выборка точек у нас будет конечной, поэтому восстановленный многочлен будет также обладать конечной степенью. Значит, при экстраполяции ошибка будет накапливаться все равно очень быстро, и никакой критерий нам уже не поможет. В равной степени если данные содержат гармоническую зависимость, то она не будет хорошо экстраполироваться ни многочленами, ни экспонентами, конечные ряды которых не могут быть периодическими. Конечно, одни типы зависимостей могут лучше или хуже экстраполироваться другими типами, но можно сказать, что если у нас в пространстве моделей нет именно того типа зависимостей, который содержится в данных, то наилучшего предсказания мы не получим.
Это же можно сказать не только о предсказании, но и, скажем, о распознавании. В случае распознавания эта проблема наиболее ярко проявляется в проблеме инвариантов. Если какие-то образы из некоторого класса удовлетворяют некоторому инварианту, то работа системы распознавания не будет достаточно хорошей, если она не может выучить именно этот инвариант. В частности, именно поэтому нейронные сети для распознавания изображений либо требуют, чтобы им сразу подавали признаки, инвариантные к геометрическим преобразованиям изображений, либо требуют выборок огромных размеров. Так, если перцептрону при обучении предъявлять распознаваемые объекты в одной части изображения, он не сможет их распознать, если их потом предъявить в другой части изображения.
Именно такого рода критика перцептронов и содержалась в знаменитой книге Минского и Паперта: они не способны строить нелокальные инварианты (выполнять соответствующее обобщение) и требуют обучающей выборки экспоненциально большого размера, чтобы научиться распознавать образ во всех его видах. Даже если перцептроны при этом не переобучаются, они не достигают главной цели эффективного обучения – выявления лежащей в основе данных закономерности, позволяющей выполнять предсказание или распознавать образы в не встречавшемся до этого виде.
Неспособность выражать закономерности произвольных видов, характерна, естественно, не только для конкретных архитектур ИНС, но и для других методов машинного обучения. Все они используют какой-то ограниченный способ представления закономерностей, например в форме конкретного семейства базисных функций, по которым ведется разложение. То же можно сказать и о символьном обучении при использовании, например, деревьев решений или наборов правил. В сложных системах, основанных на знаниях, данная проблема может быть завуалирована, но вовсе не решена.
Естественным является желание попытаться объединить разные методы, в которых учитываются разные возможные закономерности в данных. И такой подход действительно сейчас весьма популярен. Однако простое объединение неуниверсальных методов лишь немного увеличивает их возможности, поскольку вручную разработчики могут заложить лишь сравнительно небольшое количество разных семейств закономерностей.
Но можно ли заложить в систему машинного обучения способность выявлять любые возможные регулярности? Существует ли такое пространство, в котором бы конструктивно описывались произвольные закономерности, специально не предусмотренные заранее разработчиком? Такое пространство не только есть; оно еще и общеизвестно. Это пространство алгоритмов.
Требуется воспроизвести экспоненциальную зависимость? Такой алгоритм построить несложно. Нужны многочлены, гармонические функции, последовательность Фибоначчи, факториал? Есть и такие алгоритмы. Нужно распознавать классы четных и нечетных чисел? С помощью соответствующего алгоритма – легко! А теперь подумайте, насколько просто было бы решать все эти задачи одновременно с помощью ИНС. Естественно, чтобы сравнение было корректным, нужен метод, который сам строил бы все эти алгоритмы при предъявлении соответствующей обучающей выборки. Но здесь для нас главное, что в пространстве алгоритмов, по крайней мере, имеются подходящие решения всех таких задач.
Итак, чтобы система машинного обучения была универсальной, необходимо, чтобы она могла вывести любую закономерность. Современные методы машинного обучения этому требованию не удовлетворяют, поэтому сомнительно, что на их основе можно построить универсальный ИИ. Для такого ИИ в качестве «пространства всех возможных закономерностей» естественно использовать множество алгоритмов. Конечно, можно поспорить, действительно ли множество алгоритмов содержит все возможные закономерности (мы, однако, уже писали о том, что алгоритмического подхода достаточно для воплощения ИИ habrahabr.ru/post/145929/ ). В любом случае, современные методы машинного обучения работают в сильно ограниченных подпространствах алгоритмов. И если удастся «хотя бы» использовать алгоритмы произвольного вида в качестве моделей, то возможности машинного обучения невообразимо расширятся.
Поскольку подавляющее большинство методов обучения реализуется в форме алгоритмов, идея перебирать алгоритмы в качестве потенциальных решений задач обучения может показаться даже банальной. И тем лучше. Однако алгоритмов, способных воспроизвести имеющиеся данные, много (включая и алгоритм, который просто «помнит» обучающую выборку), и тот факт, что критерий длины описания позволяет выбрать наилучшее решение задачи обучения, является уже не столь очевидным.
Универсальный метод, работающий в пространстве алгоритмов и использующий критерий алгоритмической сложности для общего решения проблемы индукции (машинного обучения) был предложен Р. Соломоновым еще в 1964-м году. Правда, метод этот требует практически бесконечных вычислительных ресурсов, что вполне понятно с учетом сложности перебора алгоритмов. Не удивительно, что прагматически мыслящими исследователями он был полностью проигнорирован. Однако это не значит, что нужно искать там, где светло, а не там, где потеряли. Для создания сильного ИИ необходимо максимально приблизиться к эффективной реализации подобного универсального метода обучения, в противном случае (то есть если использовать лишь современные практические методы машинного обучения) ИИ не сможет учиться действительно чему угодно. Из понимания, в частности, этого факта и проистекает такая область исследований, как универсальный ИИ. Как приблизиться к решению проблемы – тема для отдельного непростого разговора.
Автор: aideus



