В данной статье мы будем разрабатывать (программную) модель суперскалярного процессора с OOO и фронтендом стековой машины.
Фактически, продолжение 1 & 2.
Введение
Почему стековая машина?
Филип Купман пишет: “с теоретической точки зрения стек важен сам по себе, поскольку это основной и наиболее естественный механизм для исполнения хорошо структурированного кода … стековые машины существенно эффективнее регистровых процессоров при работе с кодом, имеющим высокую модульность. Кроме того, они весьма просты и демонстрируют отличную производительность при довольно скромных требованиях к железу.”
К преимуществам стековых машин относят компактность кода, простоту компиляции и интерпретации кода, а также компактность состояния процессора.
Удачными образцами компьютеров со стековой архитектурой можно назвать Burroughs B5000 (1961...1986) и HP3000 (1974...2006). Не забудем и про советские Эльбрусы.
Так почему же стековые машины в настоящий момент вытеснены регистровыми процессорами на обочину прогресса? Причины, думается, в следующем:
- Существуют две «крайние» реализации стековых процессоров: с фиксированным аппаратным стеком и стеком, расположенным в памяти. Обе эти крайности имеют существенные изъяны: в случае стека фиксированного размера, мы имеем проблемы с компилятором и/или операционной системой, которые обязаны думать о том, что произойдет, если стек переполнится или опустеет и как отработать соответствующее прерывание. Если обработка прерывания отсутствует, мы имеем дело с микроконтроллером, обреченным на то, чтобы быть программируемым вручную. При наличии обработчика такого прерывания, аппаратный стек играет роль «окна» к памяти с быстрым доступом, при этом сдвиг этого «окна» — процедура довольно дорогая. В результате мы имеем непредсказуемое поведение программы, не позволяющее использовать такой процессор, например, в системах реального времени, хотя, с точки зрения Купмана, это как раз экологическая ниша подобных процессоров.
- В случае же стека, размещенного целиком в памяти, мы платим обращением к памяти за практически каждую исполняемую инструкцию. Таким образом, общая производительность системы ограничена сверху пропускной способностью памяти.
- Сложность процессора давно перестала быть сдерживающим фактором в развитии.
- Аппаратно реализованный стек подразумевает строгую последовательность происходящих событий, а, следовательно, и невозможность использовать неявный параллелизм программ. Если суперскалярные процессоры сами распределяют инструкции по конвейерам в соответствии с имеющимися ресурсами, а VLIW процессоры ждут, что эта работа уже выполнена за них компилятором, то для стековых машин попытка найти в коде скрытый параллелизм сталкивается с почти непреодолимыми трудностями. Иными словами, мы снова сталкиваемся с ситуацией, когда технология может дать больше, чем архитектура может себе позволить. Что странно.
- Программирование для регистровых машин более «технологично». Имея всего лишь несколько регистров общего назначения, «вручную» легко можно создать код, который будет обращаться к памяти лишь тогда, когда этого действительно нельзя избежать. Отметим, что в случае стековой машины достичь этого намного труднее. И, хотя оптимальное распределение временных переменных по регистрам является NP-полной задачей, существует несколько недорогих, но действенных эвристик, позволяющих создавать вполне приличный код за разумное время.
Были, конечно и попытки спрятать регистровую машину внутри стековой обертки, например, Ignite или ICL2900, но коммерческого успеха они не имели, т.к. фактически, только лишь ради удобства компиляции, пользователи должны были нести постоянные издержки в runtime.
Так зачем же автор вновь поднимает эту тему, что заставляет его думать, что в этой области есть перспективы, какие проблемы какими средствами он пытается решить?
Мотивы
Никто не спорит с тем, что код для стековых машин гораздо более компактен в сравнении с регистровыми архитектурами. Можно оспаривать значимость этой компактности, но факт остаётся. За счет чего достигается сжатие кода? Ведь функционально он делает то же самое, в чем фокус?
Рассмотрим простой пример, вычисление выражения x+y*z+u.
При построении дерева разбора компилятором оно выглядит так:
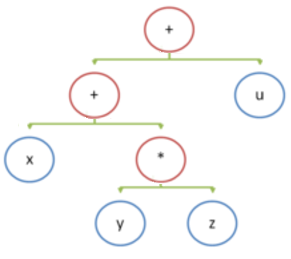
Ассемблерный код (x86) для этого выражения выглядит так:
mov eax,dword ptr [y]
imul eax,dword ptr [z]
mov ecx,dword ptr [x]
add ecx,eax
mov eax,ecx
add eax,dword ptr [u]
Для гипотетической стековой машины псевдокод таков:
push x
push y
push z
multiply
add
push u
add
Разница наглядна и очевидна, помимо 4-х обращений к памяти, сложения и умножения, в каждой инструкции регистрового процессора присутствуют идентификаторы регистров.
Но ведь этих регистров в реальности даже не существует, это фикция, которую использует супер-скалярный процессор для обозначения связи между инструкциями.
Набор регистров и операции с ними образуют архитектуру процессора и (по крайней мере для x86) исторически сложились еще в то время, когда супер-скалярных процессоров не существовало, а именами регистров обозначали вполне физические регистры.
Как известно, за время пути собака могла подрасти и идентификаторы регистров на данный момент используются для других целей. Архитектура сейчас — это скорее интерфейс между компилятором и процессором. Компилятор не знает как на самом деле устроен процессор, и может выдавать код для целой кучи совместимых устройств. А разработчики процессоров могут сосредоточиться на полезных и важных делах, создавая внешне совместимые изделия.
Какова плата за подобную унификацию?
- С точки зрения супер-скалярного процессора. Вот, например, статья от Intel, дословно:
Суперскаляр на ходу распараллеливает последовательный код. Но этот процесс распараллеливания слишком трудоемок даже для нынешних процессорных мощностей, и именно он ограничивает производительность машины. Делать это преобразование быстрее определенного количества команд за такт невозможно. Можно сделать больше, но при этом упадет тактовая чистота – такой подход, очевидно, бессмысленнен
Вот еще из любимого:
Беда не в самом суперскаляре, а в представлении программ. Программы представлены последовательно, и их нужно во время исполнения преобразовывать в параллельное выполнение. Главная проблема суперскаляра – в неприспособленности входного кода к его нуждам. Имеется параллельный алгоритм работы ядра и параллельно организованная аппаратная часть. Однако между ними, по середине, находится некая бюрократическая организация – последовательная система команд
- С точки зрения компилятора. Оттуда же:
Компилятор преобразует программу в последовательную систему команд; от той последовательности, в какой он это сделает, будет зависеть общая скорость процесса. Но компилятор не знает в точности, как работает машина. Поэтому, вообще говоря, работа компилятора сегодня – это шаманство
Компилятор прилагает титанические усилия чтобы втиснуть программу в заданное число регистров, а это число фиктивно. Весь выявленный в программе параллелизм компилятор пытается (как канат в игольное ушко) протащить сквозь ограничения архитектуры. В значительной мере безуспешно.
Что делать?
Проблема обозначена — несоответствие интерфейса/архитектуры современным требованиям.
Каковы эти (новые) требования?
- Весь известный компилятору параллелизм должен быть передан без потерь.
- Издержки на распаковку зависимостей между инструкциями должны быть минимальными.
Опять обратимся к примеру с компиляцией выражения x+y*z+u.
| х86 | стековая машина |
|---|---|
mov eax,dword ptr [y]
imul eax,dword ptr [z]
mov ecx,dword ptr [x]
add ecx,eax
mov eax,ecx
add eax,dword ptr [u]
|
push x
push y
push z
multiply
add
push u
add
|
Регистры х86 предназначены для указания связи между различными инструкциями. А что в стековой машине, как там реализованы эти зависимости? Неявно, через положение в стеке. Каждая инструкция знает число своих аргументов и ожидает перед исполнением найти их на вершине стека.
А что, если, когда мы говорим о вершине стека, это вовсе не обязательно стек данных, а, скорее, стек операций (микроопераций, моп-ов).
- Снаружи приходят стековые инструкции, но процессор на самом деле — регистровый, он умеет исполнять только вполне традиционные 'add r1 r2 r3'. Вот эти 'add ...' мы и зовем мопами. Если угодно, моп — универсальная заготовка под внутреннюю инструкцию регистрового процессора.
- У процессора есть пул мопов, изначально все они свободны, доступ по индексу.
- У мопа есть сопутствующая информация, линки — номера родительских мопов, число предков, …
- Итак, первой пришла инструкция 'push x' (x в данном случае — адрес), декодером это транслируется в 'lload R?, 0x.....', у этого мопа нет входных аргументов, только выходной.
- Моп взят из пула свободных, когда свободные мопы заканчиваются, декодер приостанавливает работу.
- Поначалу это 'lload R?, 0x.....' т.к. регистр не определен.
- Вот этот наш 'lload R?, 0x.....' мы помещаем на вершину стека индексов мопов.
- Дальше идут 'push y;push z' с ними мы проделываем то же самое. Теперь в стеке мопов три загрузки.
- Дальше идет 'multiply', для нее декодер делает моп 'lmul R? R? R?'.
- Поскольку декодер знает, что для этой инструкции нужны 2 аргумента, он берет (и удаляет) с вершины стека два верхних мопа и линкует с данным. После чего индекс мопа 'multiply' заносится на вершину стека.
- Далее идет 'add' с ним всё аналогично, только что один аргумент — загрузка из памяти, второй — умножение.
- Когда индекс мопа ушел из стека, его (моп) можно пытаться исполнить. Первый у нас 'push x', который теперь 'lload R?, 0x.....'
- Для выходного аргумента берем первый попавшийся регистр (R1, например) и помечаем его как занятый. Поскольку этот моп никого не ждет, его можно ставить в конвейер на исполнение.
- После того, как этот моп исполнился, мы извещаем наследника (только одного, это же дерево), если есть, при этом у него определяется номер регистра аргумента и уменьшается счетчик родительских мопов.
- Если входные аргументы удерживают регистр(ы), их (регистр(ы)) можно освободить
- Если счетчик ожидаемых мопов (у дочернего мопа) стал равен 0, то этот моп тоже можно перекладывать в соответствующий конвейер.
- ...
Какие бывают типы мопов?
- Операции с регистрами, например, сложение: значения двух регистров суммируются и помещаются в третий. Эти мопы бывают бинарные — перед помещением в стек из него удаляются ссылки на два верхних мопа и заносится ссылка на данный. А также унарные — смена знака, например. При создании такой операции ее ссылка замещает собой ссылку на вершине стека.
- Операции с памятью — загрузка значения из памяти в регистр и наоборот. Загрузка из памяти не имеет предшественников и просто заносится в стек мопов. Выгрузка в память убирает один элемент из стека. Загрузка из памяти добавляет в стек свою ссылку.
- Особая операция — pop, это просто указание декодеру убрать элемент с вершины стека.
- Прочие — ветвление, вызовы функций, служебные, пока не будем рассматривать
Для операций с памятью возникает особый вид связи между мопами — через адрес, например, мы загрузили значение в память и тут же читаем его из памяти в регистр. Формально между этими операциями нет связи через регистр, фактически она есть. Иными словами, будет неплохо перед чтением дождаться конца записи. Поэтому для мопов в кэше декодера необходимо отслеживать подобные зависимости. За пределами кэша эта проблема решается сериализацией через шину доступа к памяти.
Программная модель
Умозрительные конструкции отлично работают вплоть до момента попытки их реализации. Так что в дальнейшем мы будем теоретизировать параллельно с проверкой на модели.
Автором был реализован простой компилятор подмножества C, достаточного для выполнения, функции Аккермана. Компилятор выдает код для стековой машины и тут же на лету пытается его исполнить.
Не будем спешить и потренируемся на чем — нибудь простом, например
long d1, d2, d3, d4, d5, d6, d7, d8;
d1 = 1; d2 = 2;
d3 = 3; d4 = 4;
d5 = 5; d6 = 6;
d7 = 7; d8 = 8;
print_long (((d1 + d2)+(d3 + d4))+((d5 + d6)+(d7 + d8))); // отладочная функция печати
Но прежде стоит определиться с параметрами модели процессора.
- 32 целочисленных регистра
- декодируется 4 инструкции за такт
- один конвейер для работы с памятью, загрузка и выгрузка слова в/из регистра занимает 3 такта
- 2 конвейера с АЛУ, операция суммирования/вычитания занимает 3 такта, сравнения — 1 такт
Здесь и в дальнейшем показаны инструкции в момент окончания их исполнения (когда регистры уже определены) в том, конвейере, где они исполнились:
| такт | конв. памяти | конв. N1 | конв. N2 |
|---|---|---|---|
| 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 32 35 |
LLOAD r3 LLOAD r2 LLOAD r1 LLOAD r0 LLOAD r7 LLOAD r6 LLOAD r5 LLOAD r4 LSTORE r3 LSTORE r2 LSTORE r1 LSTORE r0 LSTORE r7 LSTORE r6 LSTORE r5 LSTORE r4 LLOAD r11 LLOAD r10 LLOAD r8 LLOAD r15 LLOAD r12 LLOAD r19 LLOAD r17 LLOAD r16 |
LADD r11 r10 -> r9 LADD r8 r15 -> r14 LADD r12 r19 -> r18 LADD r9 r14 -> r13 LADD r17 r16 -> r23 LADD r18 r23 -> r22 LADD r13 r22 -> r21 |
И в регистре 21 в 35 такте получаем заветное значение 36.
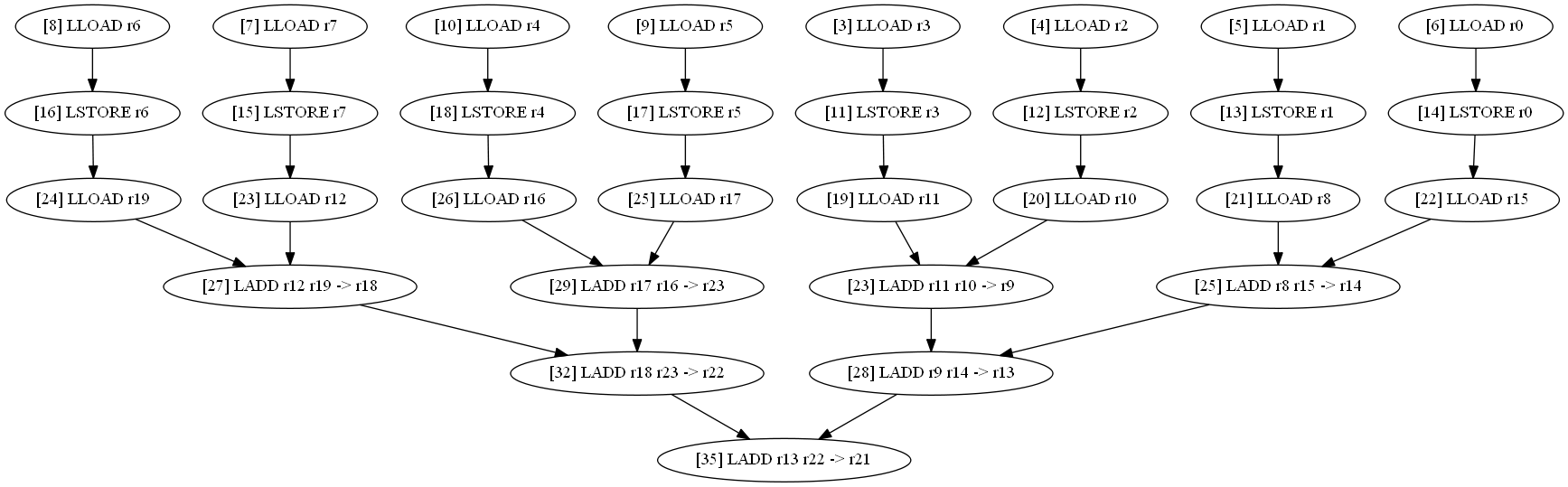 |
Данные из той же таблицы, но в виде диаграммы зависимостей мопов, в скобках [] — номер такта завершения мопа (х&y здесь не имеют смысла, значение есть только у направления стрелок).
Что мы видим?
- первые 8 инструкций LLOAD — загрузка констант
- далее 8 LSTORE — инициализация переменных константами. Может показаться странным, что они сериализовались подобным образом, ведь изначально они (LOAD&STORE) были вперемешку. Но стоит вспомнить, что загрузка константы из памяти идет 3 такта, по 4 инструкции за такт. Пока первая константа ждет загрузки, операции LSTORE в силу своей зависимости оказались в конвейере позади LLOAD. ООО в действии, кстати.
- Кажется странным, что имея 2 конвейера и очевидный параллелизм мы не смогли загрузить оба конвейера. С другой стороны, последняя загрузка из памяти закончилась через 26 тактов (8*3+2). Дерево выражения имеет глубину три по три такта на шаг. Суммарно, 26 + 9 = 35 тактов, быстрее вычислить это невозможно в принципе. Т.е. для вычисления данного кода максимально быстрым способом достаточно и одного целочисленного конвейера.
Попробуем то же, но без явной инициализации переменных.
long d1, d2, d3, d4, d5, d6, d7, d8;
print_long (((d1 + d2)+(d3 + d4))+((d5 + d6)+(d7 + d8))); // отладочная функция печати
| такт | конв. памяти | конв. N1 | конв. N2 |
|---|---|---|---|
| 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
LLOAD r3 LLOAD r2 LLOAD r0 LLOAD r7 LLOAD r4 LLOAD r11 LLOAD r9 LLOAD r8 |
LADD r3 r2 -> r1 LADD r0 r7 -> r6 LADD r4 r11 -> r10 LADD r1 r6 -> r5 LADD r9 r8 -> r15 LADD r10 r15 -> r14 LADD r5 r14 -> r13 |
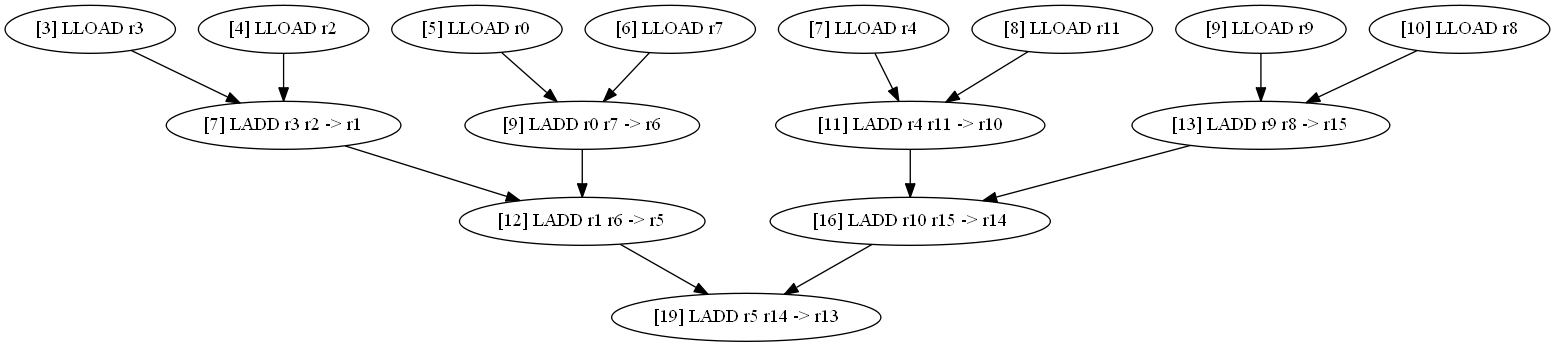 |
Вычисление заняло 8+2 + 3*3 = 19 тактов, минимальное из возможного, опять одного конвейера оказалось достаточно.
Теперь попробуем убрать все скобки и просто просуммировать переменные.
long d1, d2, d3, d4, d5, d6, d7, d8;
print_long (d1+d2+d3+d4+d5+d6+d7+d8); // отладочная функция печати
| такт | конв. памяти | конв. N1 | конв. N2 |
|---|---|---|---|
| 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
LLOAD r3 LLOAD r2 LLOAD r0 LLOAD r6 LLOAD r4 LLOAD r10 LLOAD r8 LLOAD r14 |
LADD r3 r2 -> r1 LADD r1 r0 -> r7 LADD r7 r6 -> r5 LADD r5 r4 -> r11 LADD r11 r10 -> r9 LADD r9 r8 -> r15 LADD r15 r14 -> r13 |
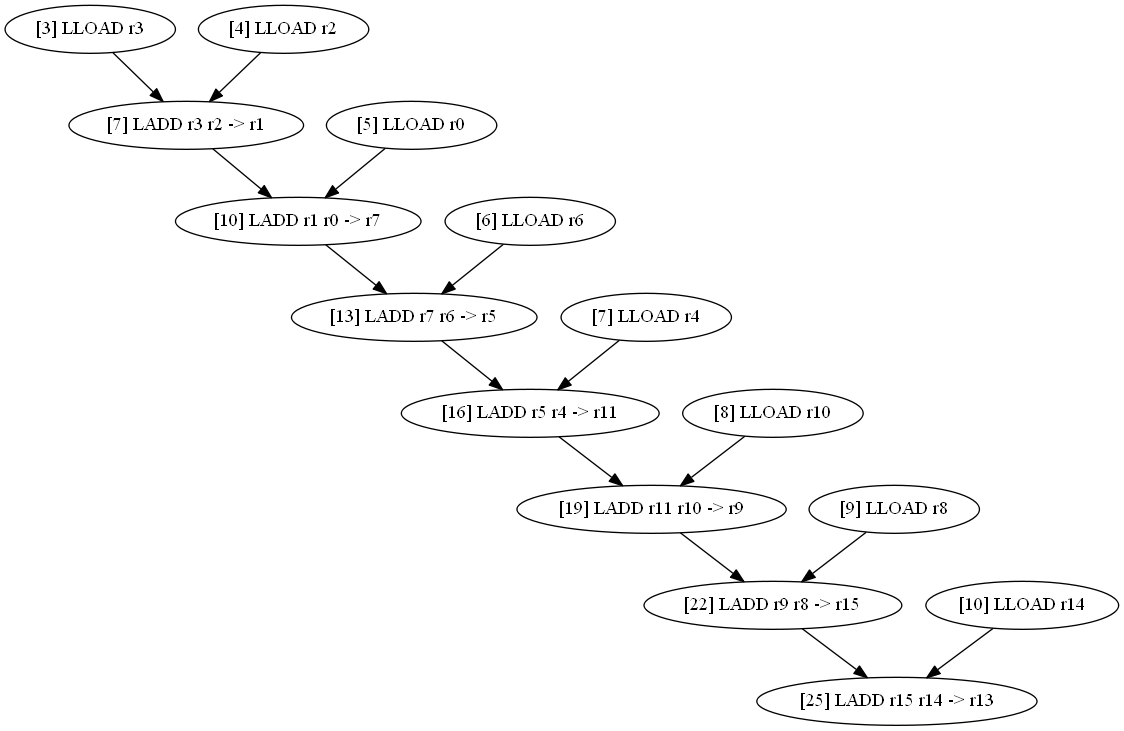 |
В данном случае есть зависимость по данным и невозможность полноценно загрузить конвейер привела к лишним 6 тактам.
Как насчет вывернуть выражение наизнанку?
long d1, d2, d3, d4, d5, d6, d7, d8;
print_long (d1+(d2+(d3+(d4+(d5+(d6+(d7+d8))))))); // отладочная функция печати
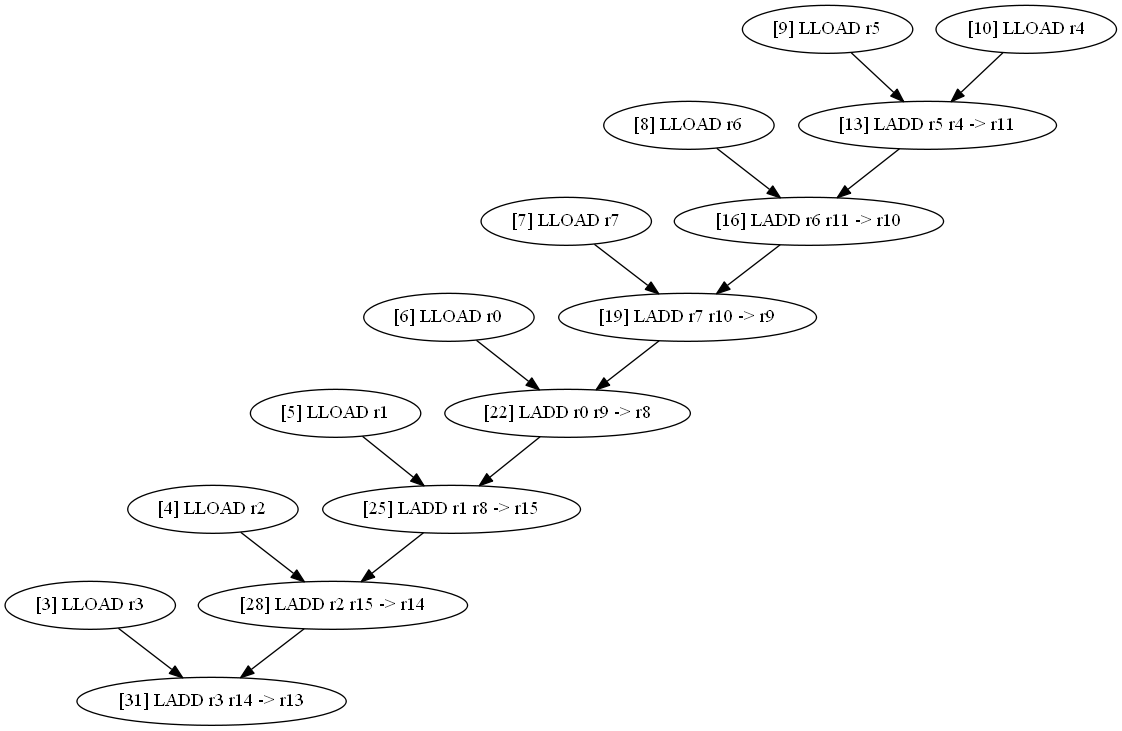 |
Это стоило еще дополнительных тактов т.к. загрузка данных идет не в оптимальном порядке.
Странно что при наличии явного параллелизма и двух целочисленных конвейеров, второй из них простаивает. Попробуем пошевелить систему. Вернемся при этом к
long d1, d2, d3, d4, d5, d6, d7, d8;
print_long (((d1 + d2)+(d3 + d4))+((d5 + d6)+(d7 + d8))); // отладочная функция печати
Попробуем увеличить скорость доступа к памяти, пусть чтение в регистр происходит за 1 такт. Забавно, но мало что изменилось. Общее время уменьшилось на 2 такта, точнее, вся картина сдвинулась вверх на 2 такта. Оно и понятно, пропускная способность памяти не изменилась, мы просто убрали задержку до получения первого результата.
Возможно, суммирование идет слишком быстро. Пусть оно делается 7 тактов вместо 3.
Общее время выросло до 29 (8+3*7) тактов, но принципиально ничего не изменилось, второй конвейер простаивает.
Попробуем просуммировать пирамидкой 16 чисел и введем 2 конвейера памяти. Общее время — 36 тактов (16/2+4*7). Второй числовой конвейер не был задействован. Числа теперь поступают парами, все 8 суммирований первого уровня стартуют с задержкой в такт и этого достаточно, чтобы всё уложилось в одном конвейере.
И только если ввести 4 конвейера памяти и разрешить 6 декодирований за такт, дело доходит до второго числового конвейера (в нем исполнились аж 3 (sic!) инструкции), общее время тем не менее — 33 такта. Т.е. эффективность собственно суммирований даже ухудшилась.
Вот уж действительно, конвейер — весьма эффективный механизм и нужны довольно веские доводы, чтобы иметь их больше одного.
Распределение регистров
В описанных выше примерах назначение регистров происходило в момент создания мопов. В результате карта использования регистров при суммировании переменных пирамидкой выглядит так (исходные параметры — 4 инструкции декодируются за такт, один конвейер памяти, по три такта на чтение и суммирование):
| 8 переменных | 16 переменных |
 |
 |
Если же назначать регистры в момент постановки инструкции в конвейер, картина выглядит заметно лучше:
| 8 переменных | 16 переменных |
 |
 |
Для контроля стоит привести и диаграмму зависимостей инструкций (8 чисел):
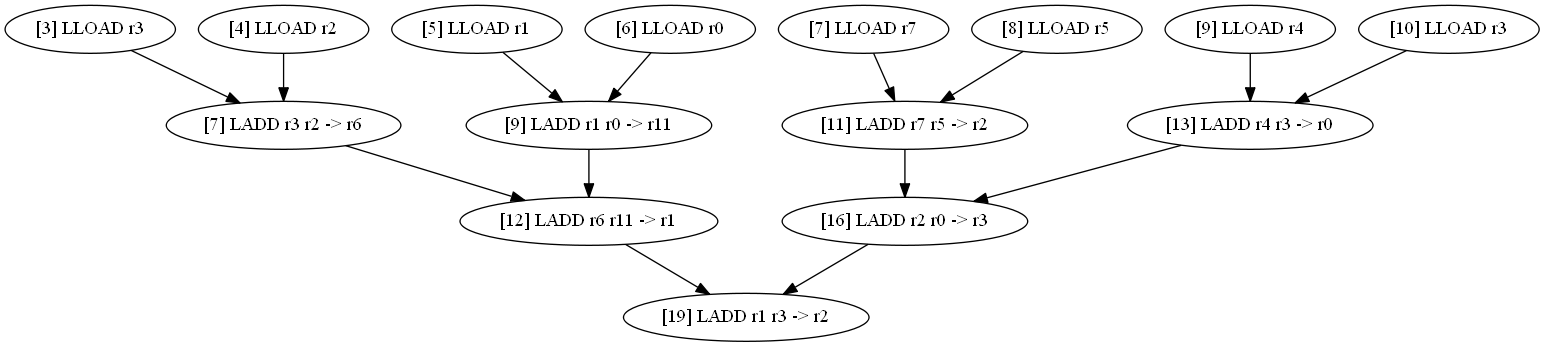 |
Вызов функций
Из общих соображений у описываемой архитектуры ожидаются проблемы с вызовом функций. В самом деле, после возврата из функции мы ожидаем и возврата состояния регистров в контексте текущей функции. В современных регистровых архитектурах для этого регистры делятся на две категории — за сохранность одних отвечает вызывающая сторона, других — вызываемая.
Но в нашей архитектуре фронтенд стековый, следовательно, компилятор может и не знать о существовании каких бы то ни было регистров. А процессор сам должен позаботиться о сохранении/восстановлении контекста, что кажется нетривиальной задачей.
Впрочем, решать эту проблему мы будем в следующей статье.
Автор: zzeng






