 В конце прошлого года Google Translate к выходу нового эпизода «Звёздных войн» добавил поддержку «Галактического языка» Ауребеш. Правда оказалось, что при выборе этого языка просто происходит перевод на английский. Если использовать Chrome или Firefox, то появляется шрифт, в котором вместо латиницы подставлены символы ауребеш, ну а в IE без особых хитростей выводится английский текст.
В конце прошлого года Google Translate к выходу нового эпизода «Звёздных войн» добавил поддержку «Галактического языка» Ауребеш. Правда оказалось, что при выборе этого языка просто происходит перевод на английский. Если использовать Chrome или Firefox, то появляется шрифт, в котором вместо латиницы подставлены символы ауребеш, ну а в IE без особых хитростей выводится английский текст.
Начал вспоминать другие примеры создания «языков чужаков». Например, язык Клингонов из «Звёздного пути» тоже основан на латинице, но при этом достаточно проработан, имеет свой синтаксис и словарь. Языки народов Средиземья из «Властелина колец» – вообще отдельная история.
А ещё существуют такие языки, как Линкос, специально разработанный Гансом Фройденталем для межпланетного общения и основанный на предположении, что математика является универсальным языком общения для любых разумных существ.
В «Плоском мире» Терри Пратчетта тоже достаточно языков, но вроде это просто переименованные земные языки. А в отношении математики, как универсального языка, более уместно упомянуть английского биолога Джека Коэна, его соавтора по книге «Наука плоского мира», который на одной конференции затронул достаточно неожиданную тему: «Почему вы думаете, что пришельцы поймут вашу математику? А вдруг у них совершенно другой способ ?»
Эту цитату я прочитал у Джеймса Нэйшина, другого участника конференции, профессора университета на Гавайях, где она и проходила. На его сайте можно найти тексты двух выступлений, в какой-то мере спровоцированных данным вопросом: «Как пришельцы делают математику» и «Логика иных планет». Может это и выглядит не очень серьёзно, особенно когда разные виды логики приписаны жителями разных планет нашей солнечной системы. Однако, вот искал возможные ссылки на одну функцию, используемую для создания обратимых вентилей, и с удивлением обнаружил её у него в разделе, посвящённом логике жителей Юпитера.
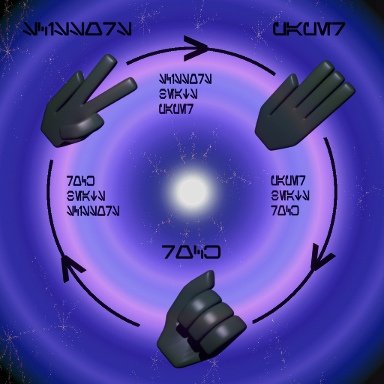
Камень, ножницы, бумага
Что же особенного в «юпитерианской логике» и как она связана с обратимыми вычислениями? Нэйшин для её описания использует набор из трёх элементов, обозначаемых символами R,P,S, которые соответствуют первым буквам английских слов для камня, ножниц и бумаги. Игра «камень, ножницы, бумага» (о ней тут тоже писали и не раз) известна и на Гавайях как «дзян-кэн». По правилам игры один из трёх предметов побеждает другой исходя из циклического набора предпочтений. Это обычно изображается на круговой диаграмме, но можно записать и в строчку:
S < — R < — P < — S

Математический символ отношения «предшествует» (Unicode 227A) использованный на картинке отсутствует во многих шрифтах, поэтому в тексте он заменён на < —
Как это связано с логикой? Известно, что если приравнять ЛОЖЬ=0, ИСТИНА=1, то «И» соответствует функции «минимум», а «ИЛИ» – «максимум». Тот же приём применяют в многозначной и нечёткой логике, так как при таком определении автоматически выполняются многие свойства обычной логики. Так что, задание отношений между элементами определяет аналоги логических операций. Правда, при циклическом наборе предпочтений между трёмя элементами некоторыми свойствами приходится пожертвовать. Что поделать, иная логика.
Таблица для аналога «ИЛИ» при таком подходе выглядит как
| Иное ИЛИ | R | P | S |
| R | R | P | R |
| P | P | P | S |
| S | R | S | S |
Таблица для операции «И» стоится аналогично
| Иное И | R | P | S |
| R | R | R | S |
| P | R | P | P |
| S | S | P | S |
Обратимые вычисления
А что с обратимыми вычислениями? О них уже тут тоже писали как, впрочем, и о троичной логике (тут, на geektimes, ещё тут) и даже вместе их пытались свести.
Обратимые вентили могут быть полезными для решения проблемы тепловыделения в процессорах следующих поколений, они тесно связаны с теорией квантовых вычислений. Да и тема сама по себе достаточно интересная. Об этом можно много где почитать, включая приведённые выше ссылки, так что постараюсь не особо распространяться на тему уже достаточно известных вещей.
Если совсем коротко, то вентиль обратим, когда значения на входах всегда можно восстановить по значениям на выходах. Для работы с двоичными данными обычно используют универсальные вентили Тоффоли или Фредкина. Оба вентиля имеют по три входа и три выхода, так как, в отличие от необратимого случая, из обратимых двоичных вентилей с двумя входами нельзя создать набор для выполнения произвольной операции над данными.
Попробуем представить обратимый аналог обычного вентиля «ИЛИ». Предположим, что у него два входа (и два выхода, раз уж он должен быть обратимым), на входы подаются двоичные значения, а один из выходов должен выдать результат операции «ИЛИ». Получается, что одно и то же значение 1 (ИСТИНА) на этом выходе может получиться при трёх разных комбинациях на входе: 11, 01, 10. Если бы второй выход мог иметь три разных значения, это можно было бы использовать для обращения такого вентиля.
Так что, уже достаточно простые оценки приводят к идее использовать троичную систему хотя бы на одном выходе. А что если попробовать работать с тремя значения на всех входах и выходах – можно ли получить обратимый вентиль, если использовать троичную логику?
Достаточно распространённой является троичная логика Лукасевича. Она может быть построена и уже упомянутым выше трюком с максимум и минимумом, если предположить, что третьему значению соответствует какое-нибудь число x, 0 < x < 1, например x = 1/2. Получаются хорошо известные троичные таблицы, для «ИЛИ»:
| «Троичное ИЛИ» | 0 | x | 1 |
| 0 | 0 | x | 1 |
| x | x | x | 1 |
| 1 | 1 | 1 | 1 |
Для «И»:
| «Троичное И» | 0 | x | 1 |
| 0 | 0 | 0 | 0 |
| x | 0 | x | x |
| 1 | 0 | x | 1 |
Предположим опять, что у нас есть троичный вентиль с двумя входами и двумя выходами. На первый выход подаётся одна из приведённых выше функций. Можно ли подобрать функцию для второго выхода, чтобы вентиль был обратимым. Оказывается, нельзя. Дело в том, что для произвольной обратимой функции в 3х3 таблице, описывающей любой вход, все значения должны встречаться по три раза.
Действительно, на вход можно подать девять возможных пар значений
00 01 0x 10 11 1x x0 x1 xx
и так как вентиль обратим, то и на выходе каждая из этих девяти пар должна появиться при одной из комбинаций на входе. Видно, что в этих парах любое значение первого (и второго) элемента встретится по три раза.
То есть, три нуля, три единицы, три икса. А вместо этого в таблице для троичного «ИЛИ» стоит только один ноль и шесть единиц. Во второй таблице для «И» наоборот, шесть нулей и одна единица, что тоже не подходит.
Поэтому, хотя обратимые троичные вентили по отдельности и троичная логика по отдельности достаточно широко используются, вместе их трудно свести. Тут и приходит на помощь «инопланетная» логика. Для наглядности заменим R,P,S на 0,1,$.

Вот таблица для «ИЛИ»
| «Иное ИЛИ» | 0 | 1 | $ |
| 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | $ |
| $ | 0 | $ | $ |
Для значений 0, 1 оно совпадает с обычным «ИЛИ», но при этом обладает уже упомянутым свойством, необходимым для создания обратимого троичного вентиля (каждое значение встречается по три раза). Ситуация с таблицей для операции «И» аналогична
| «Иное И» | 0 | 1 | $ |
| 0 | 0 | 0 | $ |
| 1 | 0 | 1 | 1 |
| $ | $ | 1 | $ |
Теперь, чтобы построить полный вариант обратимых троичных вентилей надо ещё подобрать таблицу для второго, вспомогательного выхода. В обычной арифметике для обращения функции max(a,b) на втором выходе можно было бы использовать b–a. Нечто похожее можно использовать и в нашем примере
| «Иная разность» | 0 | 1 | $ |
| 0 | 0 | $ | 1 |
| 1 | 1 | 0 | $ |
| $ | $ | 1 | 0 |
Подошло – вот так будет выглядеть полный троичный обратимый вентиль «ИЛИ»
| Вход | 00 | 01 | 0$ | 10 | 11 | 1$ | $0 | $1 | $$ |
| Выход | 00 | 11 | 0$ | 1$ | 10 | $1 | 01 | $$ | $0 |
Видно, что каждая из девяти возможных комбинаций встречается на выходе по одному разу, так что операция обратима. Действие этого вентиля можно ещё описать следующим образом: он не изменяет пары 00, 0$, переставляя по циклу семь пар (01, 11, 10, 1$, $1, $$, $0)
Так что, семикратное применение вентиля оставит любую пару значений без изменений, а обратная операция соответствует применению шести вентилей подряд. С вентилями Тоффоли и Фредкина проще, каждый из них совпадает со своим обратным.
Если подавать на вход только значения ноль и единица, то этот троичный вентиль реализует обычную логическую операцию «ИЛИ». Установив единицу на второй вход можно использовать второй выход как операцию «НЕ» от первого входа. Помимо этого, вентиль реализует операцию «разветвления» двоичного значения поданного на второй вход, если на первый подать ноль. Так что этот обратимый троичный вентиль является универсальным для работы с двоичными данными.
Пример обратимого троичного вентиля «И» аналогичен
| Вход | 00 | 01 | 0$ | 10 | 11 | 1$ | $0 | $1 | $$ |
| Выход | 00 | 01 | $$ | 0$ | 10 | 11 | $1 | 1$ | $0 |
Этот вентиль не изменяет пары 00 и 01, переставляя по циклу пары
(0$, $$, $0, $1, 1$, 11, 10, 0$)
Он тоже универсален для двоичных операций, но в отличие от «ИЛИ», одного такого вентиля не достаточно для «разветвления». Правда, выбор операции на втором выходе был достаточно произволен. Операция же на первом входе однозначно определяются выбором трёх условий: (1) выполнять нужную логическую операцию для двоичных данных, (2) соответсвовать одному из значений на входе, (3) не зависеть от их перестановки.
Выбор операции на первом входе тоже достаточно естественен и может быть использован для других моделей. Предположим, надо построить обратимый вентиль для логики Лукасевича. Проблема с этим уже была описана, некоторые значения появляются в таблице 3x3 пять раз, а их должно быть поровну, чтобы сделать обратимый вентиль.
Ещё ящерица и Спок
Тут можно применить ту же идею, что и при расширении двоичной логики до системы из трёх элементов и исходя из имеющейся проблемы с пятью повторениями в таблице для троичной логики Лукасевича (0, 1, x), нужно добавить ещё два элемента ($ и @). Другой аргумент в пользу пяти значений связан с использованием аналога разности b-a для обращения максимума и минимума: разница между тремя целыми значениями от 0 до 2 может принимать пять разных значений от -2 до 2.
Соотношения между элементами можно опять изобразить на круговой диаграмме или записать в строчку
0 <- 1 <- $ <- x <- @ <- 0 <- x <- 1 <- @ <- $ <- 0
Соответствующая игра тоже известна. Например, её версия была показана в сериале «Теория Большого взрыва» (картинка с объяснением). Соответствия можно выбрать такие: 0 -камень, 1 – бумага, $ — ножницы, @ — ящерица, x — Спок (уроженец планеты Вулкан в сериале «Звёздый путь»).
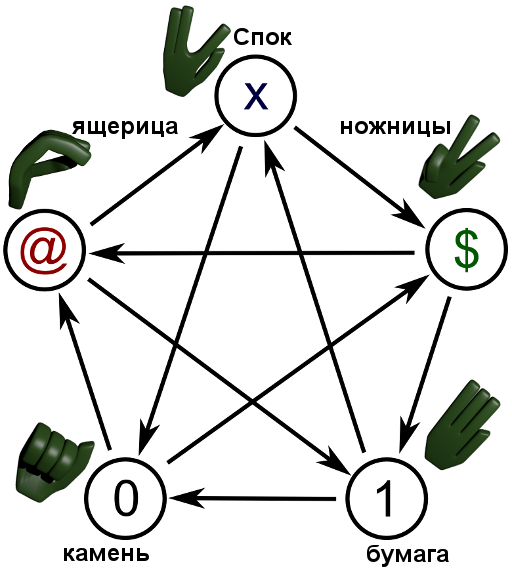
Можно продолжать и дальше; для построения похожих круговых диаграмм, особенно хорошо подходят наборы, в которых количество элементов равно простому числу.
Коллективная логика и «невозможные стрелки»
Надо сказать, что циклическая логика не такая уж «инопланетная». Один из наиболее характерных примеров связан с парадоксами Кондорсе и Эрроу относящимися к проблеме выбора. Типичное описание «парадокса голосования» можно найти в книге лауреата Нобелевской премии по экономике Кеннета Эрроу «Коллективный выбор и индивидуальные ценности».
Рассмотрим выбор из трёх альтернатив (например, выборы с тремя кандидатами) A, B, C. При этом, каждый голосующий имеет некую упорядоченную систему предпочтений. То есть, если первая альтернатива предпочтительнее второй, а вторая предпочтительная третьей, то первая тоже предпочтительнее третьей. Пример проблем с выбором, возникающий при нарушении этого критерия, тоже описан далее.
Такие упорядоченные предпочтения являются примером транзитивных отношений, а операции с аналогичным свойством ассоциативны, то есть, не зависят от расстановки скобок. Обсуждаемое ранее определение операции «ИЛИ» через задание отношений элементов хорошо согласуется с идеей выбора: операция «А ИЛИ В» – просто выбор между A и B, исходя из некого набора предпочтений (включая случай «А ИЛИ A», который, хотя и затруднительно назвать «выбором», тоже имеет вполне определённый результат, A).
Пусть кто-то полагает, что B лучше A, C лучше В (и по приведённому ранее критерию, C лучше A). Запишем этот выбор как
(1) A < B < C
Предположим, что имеются два других упорядоченных набора предпочтений
(2) B < C < A
(3) C < A < B
Обозначим доли избирателей с соответствующим набором предпочтений как P1, P2, P3. Тогда доля, считающих, что B лучше A будет P1+P3, а полагающих, что C лучше B будет P1+P2, но при этом P2+P3 думают, что A лучше C.
Если все значения P1+P2, P2+P3, P1+P3 больше половины (или, что то же самое, любая доля P1, P2, P3 меньше половины), то при голосовании B побеждает A, C побеждает B, но A побеждает C. Образуется циклическая система коллективных предпочтений, которые во избежание недоразумений обозначим уже используемым значком для отношения без свойства транзитивности
A < — B < — C < — A.
Даже при наличии у каждого индивидуума упорядоченного набора предпочтений, без транзитивности коллективный выбор уже не однозначен. Результат выборов может зависеть от порядка проведения и вообще оказаться произвольным. Далее показаны примеры трёх схем проведения выборов с разным порядком голосований, приводящие к победе любого из трёх кандидатов.
Схема 1
Первый тур: выбор между A и B, побеждает B
Второй тур: выбор между B (победившем в первом этапе) и C,
побеждает C (во втором туре и в выборах)
Схема 2
Первый тур: выбор между B и C, побеждает C
Второй тур: выбор между C и A, в выборах побеждает A
Схема 3
Первый тур: выбор между A и C, побеждает A
Второй тур: выбор между B и A, в выборах побеждает B
Эту же проблему можно проиллюстрировать как отсутствие ассоциативности в циклической системе предпочтений. Обозначим операцию выбора как ||
Тогда первые две схемы соответствуют расстановке скобок
((A || B) || C) = B || C = C,
(A || (B || C)) = A || C = A
Автор: quverty

