Решение головоломки Галакуб на Питоне

На новый год купил племяннику головоломку Галакуб. Задача собрать из разных деталей куб размером 4х4х4. Суммарный объём деталей, как раз, 4х4х4. Прежде, чем дарить надо было собрать головоломку. Красивое симметричное решение нашлось достаточно быстро. Но стало интересно единственное это решение или нет. Интуиция подсказывала, что единственное, но хотелось проверить.

Я решил по-быстрому запилить скрипт для перебора всех вариантов. В идеале нужно было успеть до новогодней речи Путина. Ситуация усугублялась тем, что код писался на Макбуке моих родителей. Поставить на него какие-то библиотеки — это задача покруче, чем написать саму программу.

Код получился на удивление красивый и понятный. Его удобно объяснять. Может быть, текст будет полезен, например, изучающим Питон.

Все детальки представлялись в виде тензоров 4х4х4.

def zero_vector():
    return [0] * 4


def zero_matrix():
    return [zero_vector() for _ in xrange(4)]


def zero_tensor():
    return [zero_matrix() for _ in xrange(4)]

Кубик кодируется буквой «Q», уголок — буквой «J», загогулина — «Z».

def parse_tensor(data):
    tensor = zero_tensor()
    lines = data.splitlines()
    for z in xrange(2):
        for y in xrange(4):
            line = lines[z * 5 + 1 + y]
            for x in xrange(4):
                if line[x] == '*':
                    tensor[z][y][x] = 1
    return tensor
    

J = parse_tensor("""
***.
*...
....
....

***.
*...
....
....

""")

Q = parse_tensor("""
**..
**..
....
....

**..
**..
....
....

""")

Z = parse_tensor("""
*...
*...
....
....

*...
***.
.**.
....

""")

>>> J
[[[1, 1, 1, 0], [1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
 [[1, 1, 1, 0], [1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
 [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
 [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]]

Чтобы удобнее смотреть на тензоры (а смотреть на них нужно будет много и внимательно), была написана функция show_tensor обратная функции parse_tensor:

def show_tensor(tensor):
    for y in xrange(4):
        for z in xrange(4):
            for x in xrange(4):
                value = tensor[z][y][x]
                print {
                    1: '*',
                    0: '.'
                }[value],
            print ' ',
        print


def show_tensors(tensors):
    for tensor in tensors:
        show_tensor(tensor)
        print


>>> show_tensors([J, Q, Z])
* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * . .   * * . .   . . . .   . . . .  
* * . .   * * . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* . . .   * . . .   . . . .   . . . .  
* . . .   * * * .   . . . .   . . . .  
. . . .   . * * .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

Дальше нужно было сгенерировать все возможные положения для каждой детальки. Вращение по оси Х и Y на 90 градусов сводятся к перестановке осей.

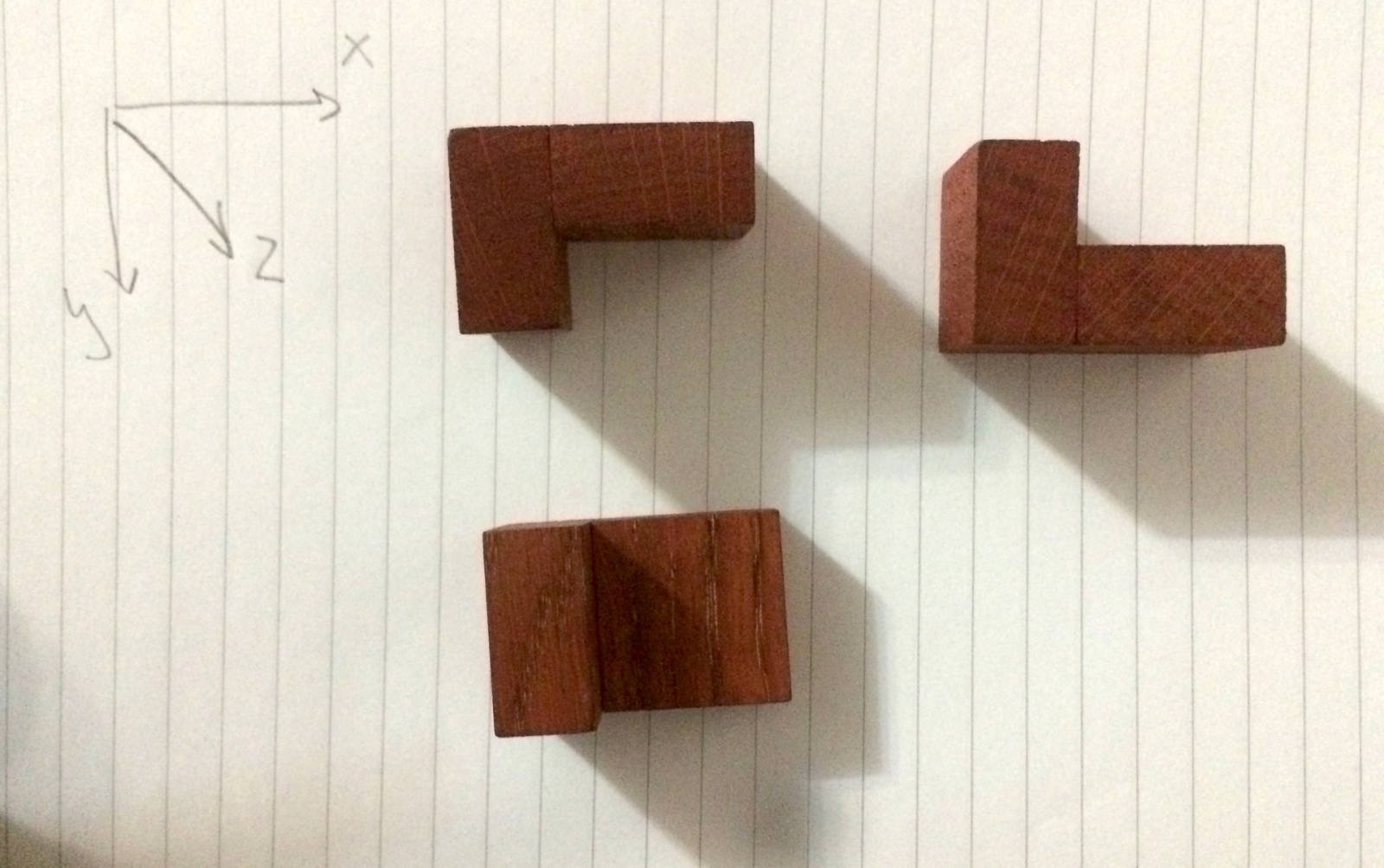
def rotate_by_x(tensor):
    rotated = zero_tensor()
    for z in xrange(4):
        for y in xrange(4):
            for x in xrange(4):
                rotated[z][y][x] = tensor[y][-z - 1][x]
    return rotated
    

def rotate_by_y(tensor):
    rotated = zero_tensor()
    for z in xrange(4):
        for y in xrange(4):
            for x in xrange(4):
                rotated[z][y][x] = tensor[x][y][-z - 1]
    return rotated

Чтобы не дублировать циклы можно завести функцию transform_tensor, она пригодится ещё не раз:

def transform_tensor(tensor, function):
    transformed = zero_tensor()
    for z in xrange(4):
        for y in xrange(4):
            for x in xrange(4):
                transformed[z][y][x] = function(tensor, x, y, z)
    return transformed


def rotate_by_x(tensor):
    return transform_tensor(tensor, lambda _, x, y, z: _[y][-z - 1][x])


def rotate_by_y(tensor):
    return transform_tensor(tensor, lambda _, x, y, z: _[x][y][-z - 1])

Посмотрим что получается:

def apply_transformation(tensor, transformation, times=1):
    for _ in xrange(times):
        tensor = transformation(tensor)
    return tensor


def show_transformation(tensor, transformation):
    show_tensors([
        tensor,
        transformation(tensor),
        apply_transformation(tensor, transformation, times=2),
        apply_transformation(tensor, transformation, times=3),
        apply_transformation(tensor, transformation, times=4),
    ])


>>> show_transformation(J, rotate_by_x)
* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . . .   . . . .   * . . .   * * * .  
. . . .   . . . .   * . . .   * * * .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   * . . .   * . . .  
. . . .   . . . .   * * * .   * * * .  

. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
* * * .   * . . .   . . . .   . . . .  
* * * .   * . . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .

>>> show_transformation(J, rotate_by_y)
* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . . .   * * . .   * * . .   * * . .  
. . . .   . . . .   . . . .   * * . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . . .   . . . .   . * * *   . * * *  
. . . .   . . . .   . . . *   . . . *  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . * *   . . * *   . . * *   . . . .  
. . * *   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

Вращение по оси Z удивительным образом можно получить вращением по оси X и Y. Только вращать надо в разные стороны, поэтому в rotate_by_y придётся ввести направление:

def rotate_by_y(tensor, direction=1):
    if direction == 1:
        function = lambda _, x, y, z: _[x][y][-z - 1]
    else:
        function = lambda _, x, y, z: _[-x - 1][y][z]
    return transform_tensor(tensor, function)


def rotate_by_z(tensor):
    return rotate_by_y(rotate_by_x(rotate_by_y(tensor, direction=-1)))

Посмотрим, что получается:

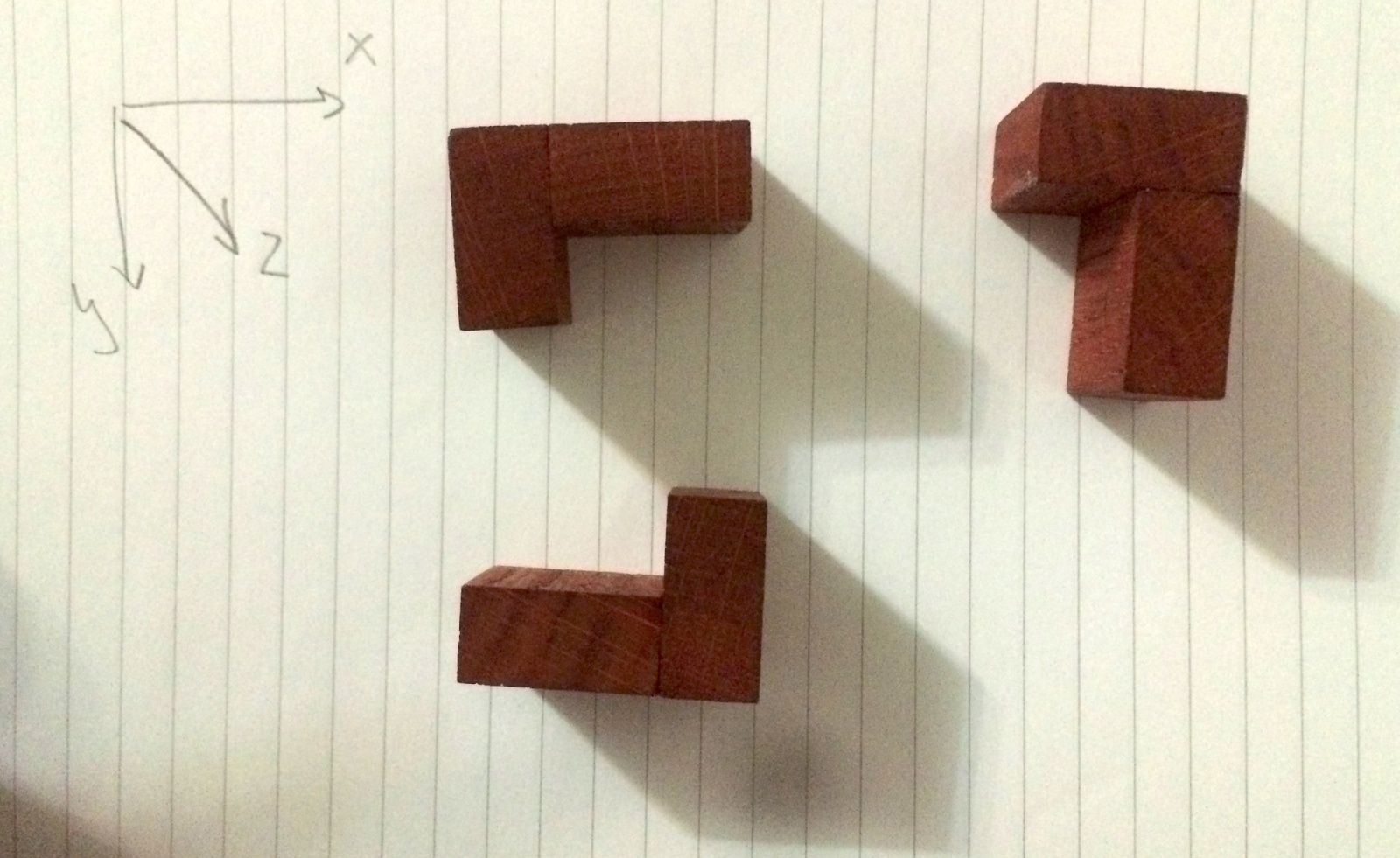
>>> show_transformation(J, rotate_by_z)
* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . * *   . . * *   . . . .   . . . .  
. . . *   . . . *   . . . .   . . . .  
. . . *   . . . *   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . *   . . . *   . . . .   . . . .  
. * * *   . * * *   . . . .   . . . .  

. . . .   . . . .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
* * . .   * * . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .

Хорошо, кроме вращений есть ещё сдвиги. Имея функцию transform_tensor, сделать сдвиг с переносом очень просто:

def shift_by_x(tensor):
    return transform_tensor(tensor, lambda _, x, y, z: _[z][y][(x + 1) % 4])

Проблема только в том, что возникают несуществующие детали:

>>> show_transformation(J, shift_by_x)
* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * . *   * * . *   . . . .   . . . .  
. . . *   . . . *   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* . * *   * . * *   . . . .   . . . .  
. . * .   . . * .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. * * *   . * * *   . . . .   . . . .  
. * . .   . * . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

Поэтому решение придётся усложнить. Будем делать сдвиг, только если есть пустое место под перенос. Нужно добавить код для вычисления проекции тензора и проверки матрицы на пустоту:

def project_tensor(tensor, function):
    projection = zero_matrix()
    for i in xrange(4):
        for j in xrange(4):
            projection[i][j] = function(tensor, i, j)
    return projection


def project_by_x(tensor):
    return project_tensor(tensor, lambda _, z, y: tensor[z][y][0])


def project_by_y(tensor):
    return project_tensor(tensor, lambda _, z, x: tensor[z][0][x])


def project_by_z(tensor):
    return project_tensor(tensor, lambda _, y, x: tensor[0][y][x])


def is_empty_matrix(matrix):
    for i in xrange(4):
        for j in xrange(4):
            if matrix[i][j]:
                return False
    return True

Теперь сдвиг будет выглядеть так:

def shift_by_x(tensor):
    if is_empty_matrix(project_by_x(tensor)):
        return transform_tensor(tensor, lambda _, x, y, z: _[z][y][(x + 1) % 4])
    return tensor

Теперь если деталь упирается в границу, ничего не происходит:

>>> show_transformation(J, shift_by_x)
* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * * .   * * * .   . . . .   . . . .  
* . . .   * . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .

Правда не получится сгенерировать все возможные детали. Нужно добавить ещё направление и каждый раз делать сдвиги в обе стороны. Финальная версия есть на Гитхабе.

Хорошо, чтобы получить все возможные положения для каждой детали, нужно перебрать все углы поворота и все размеры сдвигов:

def generate_permutations(tensor):
    for x_rotations in xrange(4):
        for y_rotations in xrange(4):
            for z_rotations in xrange(4):
                for x_shifts in xrange(3):
                    for x_direction in (-1, 1):
                        for y_shifts in xrange(3):
                            for y_direction in (-1, 1):
                                for z_shifts in xrange(3):
                                    for z_direction in (-1, 1):
                                        permutation = apply_transformation(tensor, rotate_by_x, times=x_rotations)
                                        permutation = apply_transformation(permutation, rotate_by_y, times=y_rotations)
                                        permutation = apply_transformation(permutation, rotate_by_z, times=z_rotations)
                                        permutation = apply_transformation(permutation, shift_by_x, direction=x_direction, times=x_shifts)
                                        permutation = apply_transformation(permutation, shift_by_y, direction=y_direction, times=y_shifts)
                                        permutation = apply_transformation(permutation, shift_by_z, direction=z_direction, times=z_shifts)
                                        yield permutation

Много комбинаций дублируется. Например, кубик вращать бесполезно, новых комбинаций это не добавляет:

>>> Qs = list(generate_permutations(Q))
>>> show_tensors(sample(Qs, 10))
* * . .   * * . .   . . . .   . . . .  
* * . .   * * . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

* * . .   * * . .   . . . .   . . . .  
* * . .   * * . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. * * .   . * * .   . . . .   . . . .  
. * * .   . * * .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. * * .   . * * .   . . . .   . . . .  
. * * .   . * * .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. * * .   . * * .   . . . .   . . . .  
. * * .   . * * .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

Чтобы оставить только уникальные варианты, надо определить функцию, которая ставит в соответствие тензору число. Для этого можно представить тензор 4х4х4 в виде двоичного 64-битного числа:

def hash_tensor(tensor):
    hash = 0
    index = 0
    for z in xrange(4):
        for y in xrange(4):
            for x in xrange(4):
                index += 1
                hash += tensor[z][y][x] * 2 ** index
    return hash

Теперь оставить уникальные комбинации просто:

def unique_tensors(tensors):
    hashes = set()
    for tensor in tensors:
        hash = hash_tensor(tensor)
        if hash not in hashes:
            yield tensor
        hashes.add(hash)


Zs = list(unique_tensors(generate_permutations(Z)))
Js = list(unique_tensors(generate_permutations(J)))
Qs = list(unique_tensors(generate_permutations(Q)))


>>> show_tensors(sample(Qs, 10))
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   * * . .   * * . .  
. . . .   . . . .   * * . .   * * . .  
. . . .   . . . .   . . . .   . . . .  

. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . * * .   . * * .  
. . . .   . . . .   . * * .   . * * .  

. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. * * .   . * * .   . . . .   . . . .  
. * * .   . * * .   . . . .   . . . .  

. . . .   . . . .   . * * .   . * * .  
. . . .   . . . .   . * * .   . * * .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. . . .   . . . .   . . * *   . . * *  
. . . .   . . . .   . . * *   . . * *  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  

. * * .   . * * .   . . . .   . . . .  
. * * .   . * * .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .  
. . . .   . . . .   . . . .   . . . .

За счёт того, что кубик небольшой, вариантов не так много:

>>> len(Zs), len(Js), len(Qs)
(288, 432, 27)

Самый примитивный поиск решения мог бы выглядеть так:

def solve(Zs, Js, Qs):
    for Z1 in Zs:
        for Z2 in Zs:
            for Z3 in Zs:
                for J1 in Js:
                    for J2 in Js:
                        for J3 in Js:
                            for Q1 in Qs:
                                for Q2 in Qs:
                                    if not tensors_intersect(Z1, Z2, Z3, J1, J2, J3, Q1, Q2):
                                        yield Z1, Z2, Z3, J1, J2, J3, Q1, Q2

Но это слишком тупо, нужно будет перебрать 288³432³27² вариантов. Выход есть. После того как, например, зафиксирована первая деталь, нужно игнорировать все варианты, в которых вторая деталь пересекается с первой. В решении в лоб это не так. Даже если Z1 и Z2 пересекаются, все остальные 6 подциклов отработают. Решение получше будет выглядеть так:

def solve_(path, done, hashes, todo):
    for hash in hashes:
        if not tensors_intersect(done, hash):
            if todo:
                for solution in solve_(path + [hash], union_hashes(done, hash), todo[0], todo[1:]):
                    yield solution
            else:
                yield path + [hash]


def solve(Zs, Js, Qs):
    done = zero_tensor()
    todo = [Z_hashes] * 3 + [J_hashes] * 3 + [Q_hashes] * 2
    for solution in solve_([], done, todo[0], todo[1:]):
        yield solution

Но есть ещё один нюанс. Функция tensors_intersect выглядит так:

def tensors_intersect(a, b):
    for z in xrange(4):
        for y in xrange(4):
            for x in xrange(4):
	        if a[z][y][x] and b[z][y][x]:
		    return True
    return False

Она работает долго. Выход опять есть. Функция, которая ставит тензору в соответствие число, выбрана очень удачно. Если оперировать этими числами, а не тензорами проверка на пересечение будет выглядеть так:

def tensor_hashes_intersect(a, b):
    return a & b

Поиск решений немного изменится:

def union_tensor_hashes(a, b):
    return a | b


def unhash_tensor(hash):
    tensor = zero_tensor()
    index = 0
    for z in xrange(4):
        for y in xrange(4):
            for x in xrange(4):
                index += 1
                if hash & 2 ** index:
                    tensor[z][y][x] = 1
    return tensor


def solve_(path, done, hashes, todo):
    for hash in hashes:
        if not tensor_hashes_intersect(done, hash):
            if todo:
                for solution in solve_(path + [hash], union_tensor_hashes(done, hash), todo[0], todo[1:]):
                    yield solution
            else:
                yield path + [hash]


def solve(Zs, Js, Qs):
    Z_hashes = [hash_tensor(_) for _ in Zs]
    J_hashes = [hash_tensor(_) for _ in Js]
    Q_hashes = [hash_tensor(_) for _ in Qs]
    done = hash_tensor(zero_tensor())
    todo = [Z_hashes] * 3 + [J_hashes] * 3 + [Q_hashes] * 2
    for solution in solve_([], done, todo[0], todo[1:]):
        yield [unhash_tensor(_) for _ in solution]

Запускаем:

solutions = list(solve(Zs, Js, Qs))

Ждём шесть часов и получаем 576 решений. Естественно много дублирующихся. Оставляем только уникальные и получаем 8 вариантов:

>>> show_tensors(unique_tensors(solution_tensor(_) for _ in solutions))
# # # *   # * * *   * * . .   * * . .  
# # # *   # * * *   # * . .   # * . .  
. . # #   . . * *   # * * *   # * * *  
. . # #   . . # #   # # # #   # # * *  

. . # #   . . # #   # # # *   # # # *  
. . # #   . . * *   # * * *   # * * *  
# # # #   # * * *   # * . .   * * . .  
# # * *   # * * *   # * . .   * * . .  

# # . .   # # . .   # # # #   * * # #  
# # . .   * * . .   * * * #   * * * #  
* # # #   * * * #   . . * #   . . * #  
* # # #   * * * #   . . * *   . . * *  

* * # #   * * * #   . . * #   . . * *  
# # # #   * * * #   . . * #   . . * *  
# # . .   * * . .   * * * #   * * * #  
# # . .   # # . .   * # # #   * # # #  

* * . .   # * . .   # * * *   # # * *  
* * . .   # * . .   # * * *   # # # #  
# * * *   # * * *   . . * *   . . # #  
# # # *   # # # *   . . # #   . . # #  

# # * *   # # # #   . . # #   . . # #  
# * * *   # * * *   . . * *   . . # #  
# * . .   # * . .   # * * *   # # # *  
* * . .   * * . .   # * * *   # # # *  

* # # #   * # # #   # # . .   # # . .  
* * * #   * * * #   * * . .   # # . .  
. . * *   . . * #   * * * #   # # # #  
. . * *   . . * #   * * * #   * * # #  

. . * *   . . * *   * * * #   * # # #  
. . * #   . . * #   * * * #   * # # #  
* * * #   * * * #   * * . .   # # . .  
* * # #   # # # #   # # . .   # # . .  

К сожалению это все возможные вращения того самого варианта, которое было найдено вручную. То есть у Галакуба есть только одно решение.

Автор: alexkuku

Источник