Вступление
В статье мы попробуем написать игру крестики-нолики на поле размером 10x10, игрока (человека) с ботом (компьютер) с возможностью игры через браузер, игра считается законченной, в случае одного из 3-ох исходов:
1) Победил игрок
2) Победил компьютер
3) Ничья
Такие моменты как: установка, проверка, настройка пакетов заведомо упущены, об установке Erlang'a неоднократно писали, еще, данная программа не построена по принципам OTP. Все значимые моменты я буду сопровождать схематическими картинками.
Все тесты проводились на железе:
RAM 4 GB, i5, MAC OS X
Игра корректно работает в браузерах (в остальных проверка не производилась):
Chrome 19.0.1084.56
FF 13.0.1
Safari 5.1.6 (7534.56.5)
Opera 11.64
Небольшой словарь:
Список — можно рассматривать как массив;
Символ — крестик или нолик;
Клетка, точка — ячейка для хода, имеет координаты (X;Y), где 0 < X и Y <= 10;
Направление — любое из 4 вариаций: горизонтали, вертикали, первой диагонали или второй диагонали;
Последовательность — список из 5 координат.
Сетевое взаимодействие
Для взаимодействия с пользователем, программа будет слушать порт — 8000, и ждать подключений, после того как клиент подключился, инициализировать игру.
Немаловажный момент — сторона пользователя(браузер) должна поддерживать keep-alive(постоянные) соединения, дело в том, что все взаимодействия игрока с программой реализуется посредством ajax get запросов, при такой реализации все последующие ajax get запросы будут происходят через одно соединение(socket) в неограниченном количестве*.
* Конкретной цифры после какой браузеры принудительно рвут соединение я не нашел, но однозначно могу утверждать, что до 1000 ajax get запросов через одно соединение браузеры не инициализируют закрытие сокета, а в самом худшем варианте на 1 игру понадобится 50 щапросов к серверу.
Фрагмент кода, который отвечает за обработку клиентов:
s(Port)->
spawn(
fun () ->
{ok, Socket} = gen_tcp:listen(Port, [list,{active, false},{packet, http}]),
accept_loop(Socket)
end).
accept_loop(Socket) ->
{ok, CSocket} = gen_tcp:accept(Socket),
Pid = spawn(
fun () ->
client_socket()
end),
gen_tcp:controlling_process(CSocket, Pid),
Pid ! {take_socket, Csocket}, % race condition
accept_loop(Socket).
client_socket() ->
Socket = receive {take_socket, S} -> S end,
client_loop(Socket, [], []).Алгоритм
Основная идея алгоритма основана на оценочной функции, просматриваются все пустые клетки и вычисляется коэффициент эффективности для данной клетки, это та выгода, которую мы получим, если сделаем ход в данную клетку, аналогичные действия и для соперника, какую выгоду он получит сделав ход в данную клетку.
Бзаовая формула:
G = M + A*N
M — выгода бота в данной клетки
N — выгода игрока в данной клетки
A — коэффициент агрессивности, если коэффициент увеличивать, бот будет переходить в защитную стратегию, если уменьшать, бот будет стремиться перехватить инициативу.
Теперь рассмотрим подробней:
Представим типичную игровую ситуацию:
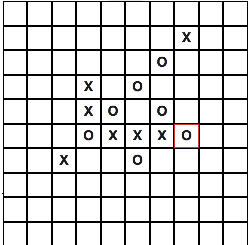
Для начала нужно сгенерировать все близлежащие координаты для одной клетки, их может быть соответственно:
3 — если клетка угловая
5 — если клетка начальная или конечная
8 — при всех остальных вариантах
Код, который отвечает за генерацию:
get_all_empty_points([]) -> [];
get_all_empty_points([Head | Tail]) -> lists:usort(get_nearby_points(Head) ++ get_all_empty_points(Tail)).
%угловые координаты
get_nearby_points({X,Y}) when X =:= 1 andalso Y =:=1 -> [{X, Y+1}, {X+1, Y+1}, {X+1, Y}];
get_nearby_points({X,Y}) when X =:= 1 andalso Y =:=10 -> [{X+1, Y}, {X+1, Y-1}, {X, Y-1}];
get_nearby_points({X,Y}) when X =:= 10 andalso Y =:=10 -> [{X-1, Y}, {X-1, Y-1}, {X, Y-1}];
get_nearby_points({X,Y}) when X =:= 10 andalso Y =:=1 -> [{X, Y+1}, {X-1, Y+1}, {X-1, Y}];
%начальные и конечные X,Y
get_nearby_points({X,Y}) when X =:= 1 -> [{X, Y-1}, {X+1, Y-1}, {X+1, Y}, {X+1, Y+1}, {X, Y+1}];
get_nearby_points({X,Y}) when Y =:= 10 -> [{X+1, Y}, {X+1, Y-1}, {X, Y-1}, {X-1, Y-1}, {X-1, Y}];
get_nearby_points({X,Y}) when X =:= 10 -> [{X, Y-1}, {X-1, Y-1}, {X-1, Y}, {X-1, Y+1}, {X, Y+1}];
get_nearby_points({X,Y}) when Y =:= 1 -> [{X-1, Y}, {X-1, Y+1}, {X, Y+1}, {X+1, Y+1}, {X+1, Y}];
%остальные точки
get_nearby_points({X,Y}) -> [{X-1, Y+1}, {X, Y+1}, {X+1, Y+1}, {X+1,Y}, {X+1, Y-1}, {X, Y-1}, {X-1, Y-1}, {X-1, Y}].
Аналогичные действия выполняем для каждой клетки в которую был сделан ход, не важно, ход это игрока или бота, после чего удаляем дубликаты, и уже имеющиеся ходы. В итоге получим список с координатами всех близлежащих клеток, точками обозначены координаты, которые мы должны получить:
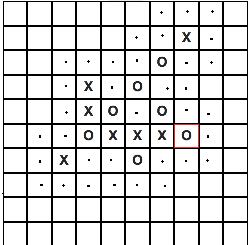
Далее нужно вычислить непосредственно выгоду хода в каждую из клеток. Рассмотрим частный вариант для одной клетки и применим для всех клеток в списке, который мы получили ранее.
Нужно сгенерировать все продолжения (ну или конец, как угодно) текущей клетки: горизонталь, вертикаль, первая диагональ, вторая диагональ, на рисунке обозначены точками — результат, который мы должны получить:

Код, который отвечает за генерация координат:
generate_point (horizontal, {X, Y}) -> [{X2,Y} || X2<-lists:seq(X-4, X+4, 1), X2 > 0, X2 < 11];
generate_point (vertical, {X, Y}) -> [{X,Y2} || Y2<-lists:seq(Y-4, Y+4, 1), Y2 > 0, Y2 < 11];
generate_point (fdiagonal, {X, Y}) -> [{X2,Y2} || X2<-lists:seq(X-4, X+4, 1), Y2<-lists:seq(Y-4,Y+4, 1), X2 > 0, Y2 > 0, X2 < 11, Y2 < 11, X2-Y2 == X-Y];
generate_point (sdiagonal, {X, Y}) -> [{X2,Y2} || X2<-lists:seq(X-4, X+4, 1), Y2<-lists:seq(Y-4,Y+4, 1), X2 > 0, Y2 > 0, X2 < 11, Y2 < 11, X2+Y2 == X+Y].Теперь рассмотрим частный вариант оценки эффективности для горизонтального направления, эти действия будут абсолютно аналогичные и для других направлений (вертикали, диагоналей).
Необходимо просмотреть все отрезки длиной в 5 клеток, для этого находим самую крайнюю точку, отсчитываем 5 клеток, а далее со сдвигом в одну клетку просматриваем еще 4 отрезка, наглядно можно посмотреть на картинке:
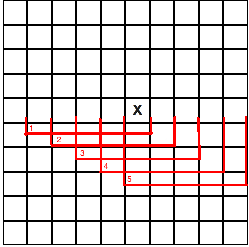
На картинке выше, показан простой пример только для наглядности, не имеющий отношения к игровой ситуации. Когда мы просматриваем отрезок из 5 клеток, мы должны выполнять некоторые инструкции для каждой из 5 последовательностей:
1) Если последовательность прерывается противоположным символом, вес данной последовательности приравнивается к нулю.
2) Если в последовательности встречается клетка с текущем символом, значение счетчика увеличивается на 1, и выполняем переход на следующую позицию.
3) Если в последовательности присутствует пустая клетка, мы ее пропускаем и переходим на следующую позицию, при этом не увеличиваем значение счетчика.
4) Если собрана последовательность из 5 текущих символов, последовательности приравнивается большой вес, если последовательность собрал бот — ее вес приравниваем к 10 000, если последовательность собрал игрок — ее вес приравниваем к 1 000, дело в том, что бот должен оценивать свою победу выше, чем свою защиту в данной ситуации.
5) Если длина последовательности равна 1, приравниваем ее к 0, это только наш мнимый ход.
Формула оценочной функции:
L
Gh = ∑ KC
i=1
L — общее количество ненулевых последовательностей
K — коэффициент, в нашем случае — 3
C — общее количество символов в последовательности, пункт 2.
Аналогично вычисляем для всех направлений: вертикали, для 2-ух диагоналей, далее суммируем все значения, это и есть выгода в численном эквиваленте:
M, N = Ghor + Gver + Gfdiag + Gsdiag
Код, который отвечает за подсчет эффективности:
calculate_point_gravity(_, _, [], _) -> [];
calculate_point_gravity(MovesX , MovesY, [Move | Rest], Aggress) ->
PGravityX = calculate(generate_point(horizontal, Move), MovesX ++ [Move], MovesY, [], Move, 1000) +
calculate(generate_point(vertical, Move), MovesX ++ [Move], MovesY, [], Move, 1000) +
calculate(generate_point(fdiagonal, Move), MovesX ++ [Move], MovesY, [], Move, 1000) +
calculate(generate_point(sdiagonal, Move), MovesX ++ [Move], MovesY, [], Move, 1000),
PGravityY = calculate(generate_point(horizontal, Move), MovesY ++ [Move], MovesX, [], Move, 10000) +
calculate(generate_point(vertical, Move), MovesY ++ [Move], MovesX, [], Move, 10000) +
calculate(generate_point(fdiagonal, Move), MovesY ++ [Move], MovesX, [], Move, 10000) +
calculate(generate_point(sdiagonal, Move), MovesY ++ [Move], MovesX, [], Move, 10000),
PGravity = PGravityY + Aggress * PGravityX,
[{PGravity, Move}] ++ calculate_point_gravity(MovesX, MovesY, Rest, Aggress).
loop(_,_,_,0, Counter) -> Counter;
loop([],_,_,_, Counter) -> Counter;
loop(_,_,_,_, opponent_point_find) -> 0;
loop([FC | RC], MovesX, MovesY, Num, Counter) ->
Res = case exist_in_list(MovesX, FC) of
true -> Counter + 1; % текущая клетка
false -> % пустая или соперника
case exist_in_list(MovesY, FC) of
true -> opponent_point_find; % соперника выход с цикла
false -> Counter % пустая, пропускаем
end
end,
loop(RC ,MovesX, MovesY, Num - 1, Res).
calculate(CList, MovesX, MovesY, Current, BreakElement, W) when Current == BreakElement -> 0;
calculate(CList, MovesX, MovesY, Current, BreakElement, W) ->
Res = loop(CList, MovesX, MovesY, 5, 0)
NewRes = case Res of
opponent_point_find -> 0;
0 -> 0;
1 -> 0; % 1 своя клетка
5 -> W; % собрана последовательность из 5,
_ -> math:pow(3, Res) % все остальное возводим в степень
end,
[Head | Rest] = CList,
NewRes + calculate(Rest, MovesX, MovesY, Head, BreakElement, W).Хочу заметить, что в функциях calculate и calculate_point_gravity, не используется хвостовая рекурсия, я не думаю, что это как-то скажется на производительности или потреблении памяти, из-за того, что количество итераций ничтожно мало.
Когда у нас подсчитан коэффициент эффективности для кажлой из клеток, мы выбираем наибольший:
lists:max(calculate_point_gravity(PlayerMovesX , PlayerMovesY, AllVariants, Agress)).Можно еще добавить случайности, но я это посчитал излишним.
Проверка
Любая игра теряет смысл, без определения двух сторон: победителя и проигравшего, но иногда и вариант с ничьей.
Теперь кратко рассмотрим алгоритм проверки на выигрыш, проверка инициализируется после каждого последующего хода игрока, и проверяет 3 исхода в порядке очереди: победа игрока, победа бота, ничья, функция проверки принимает на вход 2 аргумента, 1 — все шаги сделанные игроком, 2 — последний ход игрока.
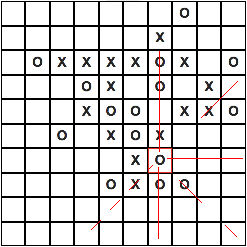
На картинке показан базовый алгоритм (там 8 лучей во все стороны, из-за сжатия не видно) — просмотр всех клеток с текущем символом и увеличением значения счетчика, но с маленьким нюансом, каждое из 4 направлений разбивается на две части: верхнюю и нижнюю, после проверки обоих частей, выполняем суммирование и прибавляем единицу, если сумма равна 5, выигрышная последовательность найдена.
Остальное
Ну и конечно же, демо:
Сложность игры динамическая, можно изменять до последующего хода, по дефолту — 0.8, чем больше коэффициент сложности — бот переходит в защитную стратегию, чем меньше — стратегия атакующая, я советую поэкспериментировать с сложностью, по-моему, бот играет достаточно хорошо в пределах [0.5, 1].
Заранее прошу прощения у людей, которые за прокси, или те, у которых порт 8000 закрыт, у меня сейчас нет возможности перекинуть игру на 80 порт.
Исходники доступны на github'e — github.com/Tremax/eTicTacToe
Клиентскую часть не рассматриваю, из-за того, что там все тривиально.
Ссылки
algolist.manual.ru/games/fiveinarow.php
Буду рад услышать Ваши отзывы.
Автор: Tremax


